Pokud je funkce
v určitém bodě diferencovatelné 
,
pak jeho přírůstek může být reprezentován jako součet dvou členů
. Tyto členy jsou nekonečně malé funkce pro 
.První člen je lineární vzhledem k 
, druhý je nekonečně malý vyšší řád než 
.Opravdu,
.
Tedy druhý termín na 
má tendenci nulovat rychleji a při hledání přírůstku funkce 
první termín hraje hlavní roli 
nebo (protože 
)
.
Definice
.
Hlavní část přírůstku funkce
na místě 
, lineární vzhledem k
,nazývaný diferenciál
funkcí
v tomto bodě a označenydynebodf(X)
. (2)
Můžeme tedy dojít k závěru: diferenciál nezávisle proměnné se shoduje s jejím přírůstkem, tzn 
.
Vztah (2) má nyní formu
(3)
Komentář . Vzorec (3) pro stručnost se často píše ve tvaru
(4)
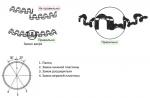
Geometrický význam diferenciálu
Uvažujme graf diferencovatelné funkce 
. body 
a patří do grafu funkce. Na místě M tečna NA ke grafu funkce, jejíž úhel s kladným směrem osy 
označovat podle 
. Pojďme kreslit rovně MN
rovnoběžně s osou Vůl
A 
rovnoběžně s osou Oj. Přírůstek funkce se rovná délce segmentu 
. Z pravoúhlého trojúhelníku 
, ve kterém 
, dostaneme
Výše uvedené úvahy nám umožňují dospět k závěru:
Funkční diferenciál
na místě 
je reprezentován přírůstkem pořadnice tečny ke grafu této funkce v jejím odpovídajícím bodě 
.
Vztah mezi diferenciálem a derivací
Zvažte vzorec (4)
.
Obě strany této rovnosti vydělíme dx, Pak
.
Tím pádem, derivace funkce je rovna poměru jejího diferenciálu k diferenciálu nezávisle proměnné.
Často tento postoj 
zacházeno jednoduše jako symbol označující derivaci funkce na argumentem X.
Pohodlný zápis pro derivát je také:
,
a tak dále.
Používají se také záznamy
,
,
zvláště vhodné, když se vezme derivát komplexního výrazu.
2. Diferenciál součtu, součinu a kvocientu.
Protože diferenciál se získá z derivace vynásobením diferenciálem nezávisle proměnné, lze při znalosti derivací základních elementárních funkcí a také pravidel pro hledání derivací dojít k podobným pravidlům pro hledání diferenciálů.
1 0 . Diferenciál konstanty je nulový
.
2 0 . Diferenciál algebraického součtu konečného počtu diferencovatelných funkcí se rovná algebraickému součtu diferenciálů těchto funkcí
3 0 . Diferenciál součinu dvou diferencovatelných funkcí se rovná součtu součinů první funkce a diferenciálu druhé a druhé funkce a diferenciálu první funkce
.
Následek. Konstantní faktor lze odečíst ze znaménka diferenciálu
.
Příklad. Najděte diferenciál funkce.
Řešení.Tuto funkci zapíšeme ve tvaru
,
pak dostaneme
.
4. Funkce zadávané parametricky, jejich derivace.
Definice
.
Funkce 
se nazývá parametricky daný, pokud obě proměnné X A
na
jsou definovány každá samostatně jako jednohodnotové funkce téže pomocné proměnné - parametrut:
Kdetse uvnitř liší 
.
Komentář
. Parametrické přiřazování funkcí je široce používáno v teoretické mechanice, kde je parametr t
označuje čas a rovnice 
jsou zákony změny v projekcích pohybujícího se bodu 
na nápravě 
A 
.
Komentář . Uvádíme parametrické rovnice kružnice a elipsy.
a) Kružnice se středem v počátku a poloměru r má parametrické rovnice:
Kde 
.
b) Napišme parametrické rovnice pro elipsu:
Kde 
.
Vyloučením parametru t Z parametrických rovnic uvažovaných přímek lze dospět k jejich kanonickým rovnicím.
Teorém
. Pokud je funkce y z argumentu
x je dáno parametricky rovnicemi 
, Kde 
A 
rozlišitelné podletfunkce a 
, Že
.
Příklad. Najděte derivaci funkce na z X dáno parametrickými rovnicemi.
Řešení. 
.
24.1. Pojem funkčního diferenciálu
Nechť funkce y=ƒ(x) má v bodě x nenulovou derivaci.
Pak podle věty o spojení funkce, její limity a nekonečně malé funkce můžeme napsat D y / D x \u003d ƒ "(x) + α, kde α → 0 pro ∆x → 0, popř. ∆y \u003d ƒ" (x) ∆х+α ∆х.
Přírůstek funkce ∆у je tedy součtem dvou členů ƒ "(х) ∆х a a ∆х, které jsou nekonečně malé při ∆x→0. V tomto případě je první člen nekonečně malá funkce stejné pořadí s ∆х, protože 
a druhý člen je nekonečně malá funkce vyššího řádu než ∆x:
Proto se nazývá první člen ƒ "(x) ∆x hlavní část přírůstku funkce ∆у.
funkční diferenciál y \u003d ƒ (x) v bodě x se nazývá hlavní část jeho přírůstku, rovná se součinu derivace funkce a přírůstku argumentu, a označuje se dу (nebo dƒ (x)):
dy \u003d ƒ "(x) ∆x. (24.1)
Diferenciál dу se také nazývá diferenciál prvního řádu. Najděte diferenciál nezávisle proměnné x, tedy diferenciál funkce y=x.
Protože y"=x"=1, pak podle vzorce (24.1) máme dy=dx=∆x, tj. diferenciál nezávisle proměnné je roven přírůstku této proměnné: dx=∆x.
Proto lze vzorec (24.1) zapsat takto:
dy \u003d ƒ "(x) dx, (24.2)
jinými slovy, diferenciál funkce se rovná součinu derivace této funkce a diferenciálu nezávisle proměnné.
Ze vzorce (24.2) vyplývá rovnost dy / dx \u003d ƒ "(x). Nyní označení
na derivaci dy/dx lze pohlížet jako na poměr diferenciálů dy a dx.
<< Пример 24.1
Najděte diferenciál funkce ƒ(x)=3x 2 -sin(l+2x).
Řešení: Podle vzorce dy \u003d ƒ "(x) dx najdeme
dy \u003d (3x 2-sin (l + 2x)) "dx \u003d (6x-2cos (l + 2x)) dx.
<< Пример 24.2
Najděte diferenciál funkce
Vypočítejte dy při x=0, dx=0,1.
Řešení:
Dosazením x=0 a dx=0,1 dostaneme
24.2. Geometrický význam diferenciálu funkce
Pojďme zjistit geometrický význam diferenciálu.
K tomu nakreslíme tečnu MT ke grafu funkce y \u003d ƒ (x) v bodě M (x; y) a uvažujeme ordinátu této tečny pro bod x + ∆x (viz obr. 138 ). Na obrázku ½ AM½ =∆x, |AM 1 |=∆y. Z pravoúhlého trojúhelníku MAB máme:
Ale podle geometrického významu derivace tga \u003d ƒ "(x). Proto AB \u003d ƒ" (x) ∆x.
Porovnáním výsledku získaného vzorcem (24.1) dostaneme dy=AB, tj. diferenciál funkce y=ƒ(x) v bodě x je roven přírůstku pořadnice tečny ke grafu funkce. v tomto bodě, když x obdrží přírůstek ∆x.
To je geometrický význam diferenciálu.
24.3 Základní diferenciální věty
Hlavní věty o diferenciálech lze snadno získat pomocí vztahu mezi diferenciálem a derivací funkce (dy=f"(x)dx) a odpovídajících vět o derivacích.
Například, protože derivace funkce y \u003d c je rovna nule, pak se diferenciál konstantní hodnoty rovná nule: dy \u003d c "dx \u003d 0 dx \u003d 0.
Věta 24.1. Diferenciál součtu, součinu a kvocientu dvou diferencovatelných funkcí je definován pomocí následujících vzorců:
Dokažme například druhý vzorec. Podle definice diferenciálu máme:
d(uv)=(uv)" dx=(uv" +vu" )dx=vu" dx+uv" dx=udv+vdu
Věta 24.2. Diferenciál komplexní funkce se rovná součinu derivace této funkce s ohledem na prostřední argument a diferenciálu tohoto prostředního argumentu.
Nechť y=ƒ(u) au=φ(x) jsou dvě diferencovatelné funkce tvořící komplexní funkci y=ƒ(φ(x)). Větou o derivaci složené funkce lze psát
y" x = y" u u" x .
Vynásobením obou částí této rovnosti dx se naučíme y "x dx \u003d y" u u "x dx. Ale y" x dx \u003d dy a u "x dx \u003d du. Poslední rovnost lze tedy přepsat jako následuje:
dy=y" u du.
Porovnáním vzorců dy=y "x dx a dy=y" u du vidíme, že první diferenciál funkce y=ƒ(x) je určen stejným vzorcem bez ohledu na to, zda je jeho argument nezávislá proměnná nebo je funkce jiného argumentu.
Tato vlastnost diferenciálu se nazývá invariance (invariance) tvaru prvního diferenciálu.
Vzorec dy \u003d y "vzhled x dx se shoduje se vzorcem dy \u003d y" u du, ale je mezi nimi zásadní rozdíl: v prvním vzorci je x nezávislá proměnná, proto dx \u003d ∆x, ve druhém vzorci a existuje funkce x , tedy obecně řečeno du≠∆u.
S pomocí definice diferenciálu a základních teorémů o diferenciálech je snadné transformovat tabulku derivací na tabulku diferenciálů.
Například: d(cosu)=(cosu)" u du=-sinudu
24.4. Diferenciální tabulka
24.5. Použití diferenciálu na přibližné výpočty
Jak již bylo známo, přírůstek ∆у funkce y=ƒ(х) v bodě x lze vyjádřit jako ∆у=ƒ"(х) ∆х+α ∆х, kde α→0 jako ∆х→0, nebo dy+α ∆x Vynecháním infinitezimálního α ∆x vyššího řádu než ∆x získáme přibližnou rovnost
∆у≈dy, (24.3)
tato rovnost je navíc tím přesnější, čím je ∆x menší.
Tato rovnost nám umožňuje s velkou přesností vypočítat přibližně přírůstek libovolné diferencovatelné funkce.
Diferenciál se obvykle nalézá mnohem snadněji než přírůstek funkce, takže vzorec (24.3) je široce používán ve výpočetní praxi.
<< Пример 24.3
Najděte přibližnou hodnotu přírůstku funkce y \u003d x 3 -2x + 1 pro x \u003d 2 a ∆x \u003d 0,001.
Řešení: Aplikujeme vzorec (24.3): ∆у≈dy=(х 3 -2х+1)" ∆х=(3х 2 -2) ∆х.
Takže ∆у» 0,01.
Podívejme se, k jaké chybě došlo při výpočtu diferenciálu funkce namísto jejího přírůstku. K tomu najdeme ∆у:
∆y \u003d ((x + ∆x) 3 -2 (x + ∆x) + 1) - (x 3 -2x + 1) \u003d x 3 + 3x 2 ∆x + 3x (∆x) 2 + ( ∆x ) 3 -2x-2 ∆x + 1-x 3 + 2x-1 \u003d ∆x (3x 2 + 3x ∆x + (∆x) 2 -2);
Absolutní chyba aproximace je rovna
|∆у-dy|=|0,010006-0,011=0,000006.
Dosazením do rovnosti (24.3) hodnot ∆у a dy získáme
ƒ(х+∆х)-ƒ(х)≈ƒ"(х)∆х
ƒ(х+∆х)≈ƒ(х)+ƒ"(х) ∆х. (24.4)
Vzorec (24.4) se používá k výpočtu přibližných hodnot funkcí.
<< Пример 24.4
Vypočítejte přibližně arctg(1,05).
Řešení: Uvažujme funkci ƒ(х)=arctgx. Podle vzorce (24.4) máme:
arctg(x+∆х)≈arctgx+(arctgx)" ∆х,
tj. 
Protože x+∆x=1,05, pak pro x=1 a ∆x=0,05 dostaneme:
Lze ukázat, že absolutní chyba vzorce (24.4) nepřesahuje hodnotu M (∆x) 2, kde M je největší hodnota |ƒ"(x)| na segmentu [x;x+∆x].
<< Пример 24.5
Jakou vzdálenost urazí těleso volným pádem na Měsíci za 10,04 s od začátku pádu. Rovnice volného pádu těla
H \u003d g l t 2 /2, g l \u003d 1,6 m / s 2.
Řešení: Je potřeba najít H(10,04). Použijeme přibližný vzorec (ΔH≈dH)
H(t+∆t)≈H(t)+H"(t) ∆t. Při t=10 sa ∆t=dt=0,04 s, H"(t)=g l t zjistíme
Úkol (pro samostatné řešení). Těleso o hmotnosti m=20 kg se pohybuje rychlostí ν=10,02 m/s. Vypočítejte přibližně kinetickou energii tělesa
24.6. Rozdíly vyšších řádů
Nechť y=ƒ(x) je diferencovatelná funkce a její argument x je nezávislé proměnné. Pak jeho první diferenciál dy=ƒ"(x)dx je také funkcí x; lze najít diferenciál této funkce.
Volá se diferenciál z diferenciálu funkce y=ƒ(x). její druhý diferenciál(nebo diferenciál druhého řádu) a označuje se d 2 y nebo d 2 ƒ(x).
Takže podle definice d 2 y=d(dy). Najděte výraz pro druhý diferenciál funkce y=ƒ(x).
Protože dx=∆x nezávisí na x, předpokládáme, že dx je při derivování konstantní:
d2 y=d(dy)=d(f"(x)dx)=(ƒ"(x)dx)" dx=f"(x)dx dx=f"(x)(dx) 2 tj. .
d 2 y \u003d ƒ "(x) dx 2. (24.5)
Zde dx 2 znamená (dx) 2 .
Rozdíl třetího řádu je definován a nalezen podobně
d 3 y \u003d d (d 2 y) \u003d d (ƒ "(x) dx 2) ≈ f" (x) (dx) 3.
A obecně je diferenciál n-tého řádu diferenciálem diferenciálu (n-1)-tého řádu: dn y=d(d n-l y)=f (n) (x) (dx) n .
Zjistíme tedy, že zejména pro n=1,2,3
respektive dostaneme:
tj. na derivaci funkce lze pohlížet jako na poměr jejího diferenciálu odpovídajícího řádu k odpovídající mocnině diferenciálu nezávisle proměnné.
Všimněte si, že všechny výše uvedené vzorce jsou platné pouze v případě, že x je nezávislá proměnná. Pokud funkce y \u003d ƒ (x), kde x - funkce nějaké jiné nezávislé proměnné, pak diferenciály druhého a vyšších řádů nemají vlastnost tvarové invariance a počítají se pomocí jiných vzorců. Ukažme si to na příkladu diferenciálu druhého řádu.
Pomocí diferenciálního vzorce produktu (d(uv)=vdu+udv) dostaneme:
d 2 y \u003d d (f "(x) dx) \u003d d (ƒ "(x)) dx + ƒ" (x) d (dx) \u003d ƒ "(x) dx dx + ƒ" (x) d 2 x, tzn.
d 2 y \u003d ƒ "(x) dx 2 + ƒ" (x) d 2 x. (24.6)
Porovnáním vzorců (24.5) a (24.6) vidíme, že v případě komplexní funkce se diferenciální formule druhého řádu změní: objeví se druhý člen ƒ "(x) d 2 x.
Je jasné, že pokud x je nezávislá proměnná, pak
d 2 x=d(dx)=d(l dx)=dx d(l)=dx 0=0
a vzorec (24.6) přechází do vzorce (24.5).
<< Пример 24.6
Najděte d 2 y, jestliže y=e 3x a x je nezávislá proměnná.
Řešení: Protože y"=3e 3x, y"=9e 3x, pak podle vzorce (24.5) máme d 2 y=9e 3x dx 2 .
<< Пример 24.7
Najděte d 2 y, jestliže y=x 2 a x=t 3 +1 at je nezávislá proměnná.
Řešení: Použijeme vzorec (24.6): od
y"=2x, y"=2, dx=3t 2 dt, d2 x=6tdt 2,
Že d 2 y=2dx 2 +2x 6tdt 2 =2(3t 2 dt) 2 +2(t 3 +1)6tdt 2 =18t 4 dt 2 +12t 4 dt 2 +12tdt 2 =(30t 4 +12t)dt 2
Jiné řešení: y=x 2, x=t 3 +1. Proto y \u003d (t 3 +1) 2. Pak podle vzorce (24.5)
d 2 y = y ¢¢ dt 2,
d2y=(30t4+12t)dt2.
Rozdíl funkce y \u003d ƒ (x) v bodě x se nazývá hlavní část jejího přírůstku, rovná se součinu derivace funkce a přírůstku argumentu, a označuje se dу (nebo dƒ (x)): dy \u003d ƒ "(x) ∆x.
Hlavní diferenciály:
Diferenciál funkce má vlastnosti podobné vlastnostem derivace.
- Konstantní diferenciál rovná se nule:
dc = 0, c = konst. - Diferenciál součtu diferencovatelných funkcí se rovná součtu diferenciálů členů:
Následek. Jestliže se dvě diferencovatelné funkce liší konstantním členem, pak jejich diferenciály jsou
d(u+c) = du (c= konst).
- produktový rozdíl dvou diferencovatelných funkcí se rovná součinu první funkce diferenciálem druhé plus součin druhé funkce diferenciálem první:
d(uv) = udv + vdu.
Následek. Konstantní faktor lze odečíst ze znaménka diferenciálu
d(cu) = cdu (c = konst).
- kvocientový diferenciál u/v dvou diferencovatelných funkcí u = u(x) a v = v(x) je definováno vzorcem
- Vlastnost nezávislosti tvaru diferenciálu na volbě nezávisle proměnné (invariance tvaru diferenciálu): diferenciál funkce je roven součinu derivace a diferenciálu argumentu, bez ohledu na to, zda tento argument je nezávislá proměnná nebo funkce jiné nezávislé proměnné.
Deriváty a diferenciály vyšších řádů.
Nechť derivaci nějaké funkce F diferencovatelné. Poté se zavolá derivace derivace této funkce druhá derivace funkcí F a označeny F". Tím pádem,
F"(X) = (F"(X))" .
Pokud je rozlišitelné ( n- 1)-tá derivace funkce F, pak ona n-tá derivace se nazývá derivát ( n- 1) derivace funkce F a označeny f(n). Tak,
f(n)(X) = (f(n-1)(X))" , n ϵ N, f(0)(X) = F(X).
Číslo n volal derivační řád.
Rozdíl n-tý řád funkcí F se nazývá diferenciál od diferenciálu ( n- 1)-tý řád stejné funkce. Tím pádem,
d n f(X) = d(d n -1 F(X)), d 0 F(X) = F(X), n ϵ N.
Li X je tedy nezávislá proměnná
dx= konst a d 2 X = d 3 X = ... = d n x = 0.
V tomto případě platí vzorec
d n f(X) = F (n) (X)(dx)n.
Deriváty n-tého řádu od základních elementárních funkcí
Spravedlivé vzorce
Aplikace derivací při studiu funkcí.
Základní derivační teorémy pro funkce:
Rolleova věta
Nechte funkci F: [A, b] → R je spojitý na segmentu [ A, b] a má v tomto segmentu konečnou nebo nekonečnou derivaci. Nechť navíc F(A) = F(b). Pak uvnitř segmentu [ A, b] má to smysl ξ takové, že F"(ξ ) = 0.
Lagrangeova věta
Pokud je funkce F: [A, b] → R je spojitý na segmentu [ A, b] a má konečnou nebo nekonečnou derivaci ve vnitřních bodech tohoto segmentu, pak takovou, že F(b) - F(A) = F"(ξ )(b - A).
Cauchyho věta
Pokud každá z funkcí F A G nepřetržitě na [ A, b] a má konečnou nebo nekonečnou derivaci na ] A, b[ a pokud navíc derivace G"(X) ≠ 0 od ] A, b[, pak takový, že vzorec
Pokud je to navíc požadováno G(A) ≠ G(b), pak podmínka G"(X) ≠ 0 lze nahradit méně pevným:
Oba jsou nerozlučně spjaty a již několik staletí se aktivně používají při řešení téměř všech problémů, které se objevily v procesu lidské vědecké a technické činnosti.
Vznik pojmu diferenciál
Poprvé vysvětlil, co je diferenciál, jeden ze zakladatelů (spolu s Isaacem Newtonem) diferenciálního počtu, slavný německý matematik Gottfried Wilhelm Leibniz. Předtím matematici 17 Čl. použil velmi nejasnou a vágní představu o nějaké nekonečně malé „nedělitelné“ části jakékoli známé funkce, která představuje velmi malou konstantní hodnotu, ale ne rovnou nule, menší než kterou hodnoty funkce prostě nemohou být. Odtud už byl jen jeden krok k zavedení konceptu infinitezimálních přírůstků argumentů funkcí a odpovídajících přírůstků funkcí samotných, vyjádřených jejich derivacemi. A tento krok učinili téměř současně oba zmínění velcí vědci.
Na základě potřeby řešit naléhavé praktické problémy mechaniky, které vědě kladl rychle se rozvíjející průmysl a technologie, vytvořili Newton a Leibniz obecné metody pro zjišťování rychlosti změny funkcí (především ve vztahu k mechanické rychlosti pohybujícího se tělesa po známé trajektorii), což vedlo k zavedení takových pojmů, jako je derivace a diferenciál funkce, a také našel algoritmus pro řešení inverzního problému, jak zjistit vzdálenost ujetou od známé (proměnné) rychlosti, která vedly ke vzniku pojmu integrál.
V pracích Leibnize a Newtona se poprvé objevila myšlenka, že diferenciály jsou hlavními částmi přírůstků funkcí Δy, úměrných přírůstkům argumentů Δx, které lze úspěšně použít k výpočtu hodnot dopis. Jinými slovy, objevili, že přírůstek funkce lze vyjádřit v libovolném bodě (v rámci její definiční oblasti) v podmínkách její derivace jako 0, mnohem rychleji než Δx samotná.
Podle zakladatelů matematické analýzy jsou diferenciály jen prvními členy ve výrazech pro přírůstky jakýchkoli funkcí. Protože ještě neměli jasně formulovaný koncept limity posloupností, intuitivně pochopili, že hodnota diferenciálu směřuje k derivaci funkce jako Δх→0 - Δу/Δх→ y"(x).
Na rozdíl od Newtona, který byl primárně fyzik a považoval matematický aparát za pomocný nástroj pro studium fyzikálních problémů, věnoval Leibniz více pozornosti samotné této sadě nástrojů, včetně systému vizuálního a srozumitelného zápisu matematických veličin. Byl to on, kdo navrhl obecně přijímaný zápis pro diferenciály funkce dy \u003d y "(x) dx, argument dx a derivace funkce ve formě jejich poměru y" (x) \u003d dy / dx .
Moderní definice
Co je diferenciál z hlediska moderní matematiky? Úzce souvisí s konceptem proměnného přírůstku. Pokud proměnná y nejprve nabude hodnoty y = y 1 a poté y = y 2 , pak se rozdíl y 2 ─ y 1 nazývá přírůstek y.
Přírůstek může být kladný. záporné a rovné nule. Slovo „přírůstek“ označujeme Δ, zápis Δy (čti „delta y“) označuje přírůstek y. takže Δу = y 2 ─ y 1 .
Jestliže hodnotu Δу libovolné funkce y = f (x) lze reprezentovat jako Δу = A Δх + α, kde A nezávisí na Δх, tj. A = konst pro dané x a člen α k ní směřuje ještě rychlejší než samotný Δx, pak první („hlavní“) člen úměrný Δx je diferenciál pro y \u003d f (x), označený dy nebo df (x) (čti „de y“, „de ef z x "). Proto jsou diferenciály „hlavními“ lineárními složkami přírůstků funkcí vzhledem k Δx.
Mechanický výklad
Nechť s = f(t) je vzdálenost od výchozí polohy (t je doba jízdy). Přírůstek Δs je dráha bodu v časovém intervalu Δt a diferenciál ds = f "(t) Δt je dráha, kterou by bod urazil za stejnou dobu Δt, kdyby si zachoval rychlost f" (t ) dosažené v době t . Pro nekonečně malé Δt se imaginární dráha ds liší od skutečné Δs o nekonečně malou hodnotu, která má vyšší řád vzhledem k Δt. Pokud rychlost v čase t není rovna nule, pak ds udává přibližnou hodnotu malého posunutí bodu.
Geometrická interpretace
Nechť přímka L je graf y = f(x). Potom Δ x \u003d MQ, Δy \u003d QM "(viz obrázek níže). Tečna MN rozděluje segment Δy na dvě části, QN a NM". První je úměrná Δх a rovná se QN = MQ∙tg (úhel QMN) = Δх f"(x), tj. QN je diferenciál dy.
Druhá část NM"udává rozdíl Δу ─dy, při Δх→0 se délka NM" zmenšuje ještě rychleji než přírůstek argumentu, tj. jeho řád malosti je vyšší než u Δх. V uvažovaném případě pro f "(x) ≠ 0 (tangens není rovnoběžná s OX) jsou segmenty QM" a QN ekvivalentní; jinými slovy, NM" klesá rychleji (jeho řádově menší je vyšší) než celkový přírůstek Δу = QM". To je vidět na obrázku (jak se M "přibližuje M, segment NM" tvoří stále menší procento segmentu QM").
Takže graficky je diferenciál libovolné funkce roven velikosti přírůstku pořadnice její tečny.
Derivační a diferenciální
Koeficient A v prvním členu výrazu pro přírůstek funkce je roven hodnotě její derivace f "(x). Nastává tedy následující vztah - dy \u003d f" (x) Δx, neboli df (x) \u003d f "(x) Δx.
Je známo, že přírůstek nezávislého argumentu je roven jeho diferenciálu Δх = dx. V souladu s tím můžete napsat: f "(x) dx \u003d dy.
Hledání (někdy nazývané "řešení") diferenciálů se provádí podle stejných pravidel jako u derivací. Jejich seznam je uveden níže.
Co je univerzálnější: přírůstek argumentu nebo jeho diferenciál
Zde je nutné uvést několik vysvětlení. Znázornění diferenciálu hodnotou f "(x) Δx je možné při uvažování x jako argumentu. Funkce však může být komplexní, ve které x může být funkcí nějakého argumentu t. Pak vyjádření diferenciálu výrazem f "(x) Δx je zpravidla nemožné; kromě případu lineární závislosti x = at + b.
Pokud jde o vzorec f "(x) dx \u003d dy, pak v případě nezávislého argumentu x (pak dx \u003d Δx) a v případě parametrické závislosti x na t představuje diferenciál.
Například výraz 2 x Δx představuje pro y = x 2 jeho diferenciál, když x je argument. Položme nyní x= t 2 a vezměme t jako argument. Potom y = x 2 = t 4 .
Tento výraz není úměrný Δt, a proto nyní 2xΔх není diferenciál. Lze to zjistit z rovnice y = x 2 = t 4 . Ukázalo se, že je roven dy=4t 3 Δt.
Vezmeme-li výraz 2xdx, pak představuje diferenciál y = x 2 pro libovolný argument t. Při x= t 2 skutečně dostáváme dx = 2tΔt.
To znamená, že 2xdx = 2t 2 2tΔt = 4t 3 Δt, tj. výrazy diferenciálů zapsané v termínech dvou různých proměnných se shodovaly.
Nahrazení přírůstků diferenciály
Pokud f "(x) ≠ 0, pak Δу a dy jsou ekvivalentní (pro Δх→0); pokud f "(x) = 0 (což znamená dy = 0), nejsou ekvivalentní.
Pokud například y \u003d x 2, pak Δy \u003d (x + Δx) 2 ─ x 2 \u003d 2xΔx + Δx 2 a dy \u003d 2xΔx. Pokud x=3, pak máme Δу = 6Δх + Δх 2 a dy = 6Δх, které jsou ekvivalentní díky Δх 2 →0, při x=0 nejsou hodnoty Δу = Δх 2 a dy=0 ekvivalentní.
Tato skutečnost spolu s jednoduchou strukturou diferenciálu (tj. linearita vzhledem k Δx) se často používá v přibližných výpočtech za předpokladu, že Δy ≈ dy pro malé Δx. Najít diferenciál funkce je obvykle jednodušší než vypočítat přesnou hodnotu přírůstku.
Máme například kovovou krychli o hraně x = 10,00 cm, při zahřátí se hrana prodlouží o Δx = 0,001 cm O kolik se zvětšil objem V krychle? Máme V \u003d x 2, takže dV \u003d 3x 2 Δx \u003d 3 10 2 0 / 01 \u003d 3 (cm 3). Nárůst objemu ΔV je ekvivalentní diferenciálnímu dV, takže ΔV = 3 cm 3 . Úplný výpočet by dal ΔV = 10,01 3 ─ 10 3 = 3,003001. Ale v tomto výsledku jsou všechny údaje kromě prvního nespolehlivé; takže to každopádně musíte zaokrouhlit na 3 cm 3.
Je zřejmé, že takový přístup je užitečný pouze tehdy, pokud je možné odhadnout velikost zavedené chyby.
Funkční diferenciál: Příklady
Zkusme najít diferenciál funkce y = x 3 bez nalezení derivace. Zvyšme argument a definujme Δу.
Δy \u003d (Δx + x) 3 ─ x 3 \u003d 3x 2 Δx + (3xΔx 2 + Δx 3).
Zde koeficient A= 3x 2 nezávisí na Δх, takže první člen je úměrný Δх, zatímco druhý člen 3xΔх 2 + Δх 3 při Δх→0 klesá rychleji než přírůstek argumentu. Proto člen 3x 2 Δx je diferenciál y = x 3:
dy \u003d 3x 2 Δx \u003d 3x 2 dx nebo d (x 3) \u003d 3x 2 dx.
V tomto případě d(x 3) / dx \u003d 3x 2.
Nalezněme nyní dy funkce y = 1/x z hlediska její derivace. Potom d(1/x) / dx = ─1/x2. Proto dy = ─ Δх/х 2 .
Diferenciály základních algebraických funkcí jsou uvedeny níže.
Přibližné výpočty pomocí diferenciálu
Často není obtížné vypočítat funkci f (x), stejně jako její derivaci f "(x) pro x=a, ale není snadné udělat totéž v okolí bodu x=a. přibližné vyjádření přichází na pomoc
f (a + Δх) ≈ f "(a) Δх + f (a).
Udává přibližnou hodnotu funkce při malých přírůstcích Δх prostřednictvím jejího diferenciálu f "(a)Δх.
Proto tento vzorec dává přibližný výraz pro funkci v koncovém bodě úseku délky Δx jako součet její hodnoty v počátečním bodě tohoto úseku (x=a) a diferenciálu ve stejném počátečním bodě. Chyba této metody určení hodnoty funkce je znázorněna na obrázku níže.
Známý je však i přesný výraz pro hodnotu funkce pro x=a+Δх daný vzorcem pro konečné přírůstky (nebo jinými slovy Lagrangeovým vzorcem)
f (a + Δх) ≈ f "(ξ) Δх + f (a),
kde bod x = a + ξ je na úsečce od x = a do x = a + Δx, ačkoli jeho přesná poloha není známa. Přesný vzorec umožňuje odhadnout chybu přibližného vzorce. Pokud do Lagrangeova vzorce dosadíme ξ = Δх /2, pak sice přestane být přesný, ale obvykle dává mnohem lepší aproximaci než původní výraz přes diferenciál.
Odhadování chyby vzorců aplikací diferenciálu
V zásadě jsou nepřesné a vnášejí do naměřených dat odpovídající chyby. Vyznačují se mezní nebo stručně řečeno mezní chybou - kladným číslem, zjevně přesahující tuto chybu v absolutní hodnotě (nebo alespoň rovné). Limita se nazývá podíl jejího dělení absolutní hodnotou měřené hodnoty.
Nechť se použije přesný vzorec y= f (x) pro výpočet funkce y, ale hodnota x je výsledkem měření, a proto vnáší do y chybu. Poté, abyste našli omezující absolutní chybu │Δу│funkce y, použijte vzorec
│Δу│≈│dy│=│ f "(x)││Δх│,
kde │Δх│ je mezní chyba argumentu. Hodnota │Δу│ by měla být zaokrouhlena nahoru, protože nepřesné je samotné nahrazení výpočtu přírůstku výpočtem diferenciálu.
