Припустимо, що для довільного перерізу (рис. 1.13) моменти інерції щодо координатних осей z та y відомі, а також відомий відцентровий момент інерції Izy. Потрібно встановити залежності моментів інерції щодо осей 11 zy, повернутих на кут по відношенню до вихідних осях z і y (рис. 1.13). Вважатимемо кут позитивним, якщо поворот координатної системи відбувається проти ходу годинникової стрілки. Нехай для перерізу IzI. yДля вирішення поставленого завдання знайдемо залежність між координатами майданчика dA у вихідних та повернутих осях. З рис.1.13 випливає: З трикутника з трикутника З огляду на це отримуємо Аналогічно для координати y1 отримуємо Враховуючи, що остаточно маємо 1Скориставшись отриманими залежностями (1.23), (1.24) і виразами для моментів інерції перерізу (1.8), (1.9) ), визначаємо момент інерції щодо нових (повернутих) осей z1 і y1: Аналогічно Відцентровий момент інерції I щодо повернених осей визначиться залежністю Після розкриття дужок отримаємо Складаючи, отримуємо Сума моментів інерції щодо взаємно перпендикулярних осей не змінюється при їх повороті і дорівнює . Віднімаючи (1.27) з (1.26) отримуємо Формула (1.30) може служити для обчислення відцентрового моменту інерції щодо осей z та y , за відомими моментами інерції щодо осей z , y та z1, y1, а формула (1.29) – для перевірки обчислень моментів інерції складних перерізів 1.8. Головні осі та головні моменти інерції перерізу Зі зміною кута (див. рис. 1.13) змінюються і моменти інерції. За деяких значень кута 0 моменти інерції мають екстремальні значення. Осьові моменти інерції, що мають максимальні та мінімальні значення, називаються головними осьовими моментами інерції перерізу. Осі, щодо яких осьові моменти інерції мають максимальні та мінімальні значення, є головними осями інерції. З іншого боку, як зазначалося вище, головні осі, це осі щодо яких відцентровий момент інерції перерізу дорівнює нулю. Для визначення положення головних осей для перерізів довільної форми візьмемо першу похідну від I і прирівняємо її нулю: Звідки Ця формула визначає положення двох осей, щодо однієї з яких осьовий момент інерції максимальний, а щодо іншої - мінімальний. Необхідно зауважити, що формула (1.31) може бути отримана (1.28), прирівнявши її нулю. Якщо підставити значення кута, що визначається з виразу (1.31), (1. 26) і (1.27), то після перетворення отримаємо формули, що визначають головні осьові моменти інерції перерізу. За своєю структурою ця формула аналогічна формулі (4.12), що визначає головні напруги (див. Розд. 4.3). Якщо IzI, то, виходячи з досліджень другої похідної, випливає, що максимальний момент інерції Imax має місце щодо головної осі, поверненої на кут по відношенню до осі z, а мінімальний момент інерції – відносно іншої головної осі, розташованої під кутом 0 Якщо ІІ, що все змінюється навпаки. Значення головних моментів інерції Imax і I можуть бути обчислені і залежно (1.26) і (1.27), якщо підставити в них замість значення. При цьому саме собою вирішується питання: щодо якої головної осі виходить максимальний момент інерції та щодо якої осі – мінімальний? Необхідно звернути увагу, що якщо для перерізу головні центральні моменти інерції щодо осей z і y рівні, то цей переріз будь-яка центральна вісь є головною і всі головні центральні моменти інерції однакові (коло, квадрат, шестикутник, рівносторонній трикутник і ін.). Це легко встановлюється із залежностей (1.26), (1.27) та (1.28). Справді, припустимо, що з якогось перерізу осі z і y ─ головні центральні осі і ще I. yТогда з формул (1.26) і (1.27) отримаємо, що Izy , 1а з формули (1.28) переконаємося, що 11 е. будь-які осі є головними центральними осями інерції такої постаті. 1.9. Поняття про радіус інерції Момент інерції перерізу щодо будь-якої осі можна подати у вигляді добутку площі перерізу на квадрат деякої величини, яка називається радіусом інерції площі перерізу де iz ─ радіус інерції щодо осі z . Тоді з (1.33) випливають: Головним центральним осям інерції відповідають головні радіуси інерції: 1.10. Моменти опору Розрізняють осьові та полярні моменти опору. 1. осьовим моментом опору називається відношення моменту інерції щодо даної осі до відстані до найбільш віддаленої точки поперечного перерізу від цієї осі. Осьовий момент опору щодо осі z: а щодо осі y: max де ymax та zmax─ відповідно відстані від головних центральних осей z та y до точок найбільш віддалених від них. При розрахунках використовуються головні центральні осі інерції та головні центральні моменти, тому під Iz та Iy у формулах (1.36) та (1.37) розумітимемо головні центральні моменти інерції перерізу. Розглянемо обчислення моментів опору деяких простих перерізів. 1. Прямокутник (див. рис. 1.2): 2. Коло (див. рис. 1.8): 3. Трубчастий перетин кільцевий (рис. 1.14): . Для прокатних профілів моменти опору наводяться в таблицях сортаменту і їх визначення немає необхідності (див. дод. 24 – 27). 2. Полярним моментом опору називається відношення полярного моменту інерції до відстані від полюса до найбільш віддаленої точки перерізу max 30 Як полюс зазвичай приймається центр тяжкості перерізу. Наприклад, для суцільного круглого перерізу (рис. 1.14): Для трубчастого круглого перерізу. Осьові моменти опору Wz і Wy характеризують суто з геометричної сторони опір стрижня (балки) деформації вигину, а полярний момент опору W опір крученню.

Обчислимо моменти інерції фігури довільної форми щодо осей, повернутих щодо заданих осей та
на кут (Рис.4.14)

Нехай моменти інерції щодо осей
і
відомі. Виберемо довільний майданчик
і висловимо її координати у системі осей
і
через координати в колишніх осях
і
:

Знайдемо осьові та відцентрові моменти інерції фігури щодо повернутих осей
і
:

Приймаючи до уваги, що

;
і
,

Так само встановимо:

Відцентровий момент інерції набуває вигляду:

. (4.30)

Виразимо осьові моменти через синус та косинус подвійного кута. Для цього введемо такі функції:

. (4.31)

Підставляючи (4.31) до формул (4.27) і (4.28), отримаємо:

Якщо скласти вирази для осьових моментів інерції (4.32) та (4.33), то отримаємо:

Умова (4.34) є умовою інваріантності суми осьових моментів інерції щодо двох взаємно перпендикулярних осей, тобто. сума осьових моментів інерції щодо двох взаємно перпендикулярних осей не залежить від величини кута повороту осей і є постійною величиною.Раніше ця умова була отримана на тій підставі, що сума осьових моментів інерції щодо двох взаємно перпендикулярних осей дорівнювала величині полярного моменту інерції щодо точки перетину цих осей.

Досліджуємо рівняння для моменту інерції на екстремум і знайдемо таке значення кута , коли момент інерції досягне екстремальної величини. Для цього візьмемо першу похідну від моменту інерції по кутку (вираз (4.32)) та результат прирівняємо нулю. При цьому покладемо
.

(4.35)

Вираз у дужках є відцентровим моментом інерції щодо осей, нахилених до осі.
під кутом . Щодо цих осей відцентровий момент інерції дорівнює нулю:

, (4.36)

а це означає, нові осі є головними осями.

Раніше було визначено, що головними осями інерції є осі, щодо яких відцентровий момент інерції дорівнює нулю. Зараз це визначення можна розширити – це осі, щодо яких осьові моменти інерції мають екстремальні значення. Моменти інерції щодо цих осей називаються головними моментами інерції.

Знайдемо становище основних осей інерції. З виразу (4.36) можна отримати:

. (4.37)

Отримана формула дає для кута два значення: і
.

Отже, є дві взаємно перпендикулярні осі, щодо яких моменти інерції мають екстремальні значення. Як зазначалося вище, такі осі називаються головними осями інерції. Залишається встановити, щодо якої з осей момент інерції досягає максимального значення, а який – мінімального значення. Вирішити це завдання можна шляхом дослідження другої похідної від виразу (4.32) по кутку . Підставивши у вираз для другої похідної значення кута або
і досліджуючи знак другої похідної, можна будувати висновки про те, який із кутів відповідає максимальному моменту інерції, який – мінімальному. Нижче будуть наведені формули, які дадуть однозначне значення куту .

Знайдемо екстремальні значення моментів інерції. Для цього перетворюємо вираз (4.32), виносячи за дужку
:

Використовуємо відому з тригонометрії функцію і підставимо вираз (4.37), отримаємо:

. (4.39)

Підставляючи у формулу (4.38) вираз (4.39) і роблячи необхідні обчислення, отримуємо два вирази для екстремальних моментів інерції, які не включають кут нахилу осей :

; (4.40)

. (4.41)

З формул (4.40) та (4.41) видно, що величини головних моментів інерції визначаються безпосередньо через моменти інерції щодо осей
і
. Тому їх можна визначати, не знаючи положення найголовніших осей.

Знаючи екстремальні значення моментів інерції
і
можна крім формули (4.37) визначати становище основних осей інерції.

Наведемо без висновку формули, що дозволяють знаходити кути і між віссю
та головними осями:

;
(4.42)

Кут визначає положення осі, щодо якої момент інерції досягає максимальної величини (
), кут визначає положення осі, щодо якої момент інерції досягає мінімальної величини (
).

Введемо ще одну геометричну характеристику, яка називається радіусом інерції перерізу. Позначається ця характеристика буквою і може бути обчислена щодо осей
і
наступним чином:

;
(4.43)

Радіус інерції знаходить широке застосування у завданнях опору матеріалів та його застосування буде розглянуто у наступних розділах курсу.

Розглянемо кілька прикладів розрахунків конструкцій з урахуванням повороту осей та з використанням радіуса інерції перерізу.

Приклад 4.7.Моменти інерції перерізу прямокутної форми щодо головних осей рівні відповідно
см 4 ,
см 4 . При повороті на 45 0 моменти інерції щодо нових осей виявилися однаковими. Чому дорівнює їхня величина?

Для вирішення задачі скористаємося виразом (4.28) з урахуванням того, що відцентровий момент інерції щодо головних осей дорівнює нулю:

Підставимо у формулу (а) чисельні значення для моментів інерції та кута повороту осей:

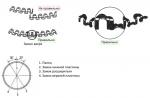
приклад 4.8.У якої з постатей (Рис.4.15), що мають однакову площу, радіус інерції щодо осі , Чи буде найбільшим? Визначити найбільший радіус інерції перерізу щодо осі .

1. Знайдемо площу кожної з фігур та розміри перерізів. Площа фігур дорівнює третьої фігури см 2 .

Діаметр першого перерізу знайдемо з виразу:

див.

Розмір сторони квадрата:

Основа трикутника:

див.

2. Знаходимо моменти та радіуси інерції кожного із перерізів щодо центральної осі .

Для перерізу круглої форми:

см 4;
див.

Для перерізу квадратної форми:

см 4;
див.

Для перерізу прямокутної форми:

;

Для перерізу трикутної форми:

см 4;
див.

Найбільший радіус інерції виявився у перерізу прямокутної форми і дорівнює він
див.

Головні осі та головні моменти інерції

При повороті осей координат відцентровий момент інерції змінює знак, отже, існує таке положення осей, у якому відцентровий момент дорівнює нулю.

Осі, щодо яких відцентровий момент інерції перерізу перетворюється на нуль, називаютьсяголовними осями , а головні осі, що проходять через центр тяжкості перерізу -головними центральними осями інерції перерізу.

Моменти інерції щодо головних осей перетину інерції називаютьсяголовними моментами інерції перерізуі позначаються через I1 та I2 причому I1>I2 . Зазвичай, говорячи про основні моменти, мають на увазі осьові моменти інерції щодо головних центральних осей інерції.

Припустимо, що осі u та v головні. Тоді

Звідси

.

(6.32)

Рівняння (6.32) визначає положення основних осей інерції перерізу в даній точці щодо вихідних осей координат. При повороті осей координат змінюються також осьові моменти інерції. Знайдемо положення осей, щодо яких осьові моменти інерції досягають екстремальних значень. Для цього візьмемо першу похідну від Iu по α і прирівняємо її нулю:

звідси

.

До того ж результату наводить і умова dIv/dα. Порівнюючи останній вираз з формулою (6.32), приходимо до висновку, що головні осі інерції є осями, щодо яких осьові моменти перетину інерції досягають екстремальних значень.

Для спрощення обчислення основних моментів інерції формули (6.29) - (6.31) перетворюють, виключаючи їх за допомогою співвідношення (6.32) тригонометричні функції:

.

(6.33)

Знак плюс перед радикалом відповідає більшому I1 , а знак мінус - меншому I2 з моментів інерції перерізу.

Вкажемо на одне важливе властивість перерізів, які мають осьові моменти інерції щодо головних осей однакові. Припустимо, що осі y та z головні (Iyz = 0), а Iy = Iz . Тоді згідно з рівностями (6.29) - (6.31) при будь-якому куті повороту осейα відцентровий момент інерції Iuv = 0, а осьові Iu = Iv.

Отже, якщо моменти інерції перерізу щодо головних осей однакові, то всі осі, що проходять через ту ж точку перерізу, є головними та осьові моменти інерції щодо всіх цих осей однакові: Iu=Iv=Iy=Iz. Цю властивість мають, наприклад, квадратні, круглі, кільцеві перерізи.

Формула (6.33) аналогічна формулам (3.25) для основних напруг. Отже, головні моменти інерції можна визначати графічним способом методом Мора.

Зміна моментів інерції при повороті осей координат

Припустимо, що задана система осей координат та відомі моменти інерції Iz , Iy та Izy фігури щодо цих осей. Повернемо осі координат на деякий кутα проти годинникової стрілки та визначимо моменти інерції тієї ж фігури щодо нових осей координат u та v.

Мал. 6.8.

З рис. 6.8 слід, що координати будь-якої точки в обох системах координат пов'язані між собою співвідношеннями

Момент інерції

Отже,

	(6.29)
	(6.30)

Відцентровий момент інерції

.

(6.31)

З отриманих рівнянь видно, що

,

т. е. сума осьових моментів інерції при повороті осей координат залишається величиною незмінною. Тому, якщо щодо будь-якої осі момент інерції досягає максимуму, то щодо перпендикулярної до неї осі він має мінімальне значення.

Обчислимо моменти інерції J u , J v та J uv:

Склавши перші дві формули (3.14), отримаємо J u + J v= J z+ J y, тобто. за будь-якого повороту взаємно перпендикулярних осей сума осьових моментів інерції залишається величиною постійної (інваріантом).

Головні осі та головні моменти інерції

Досліджуємо функцію J u(a) на екстремум. Для цього прирівняємо похідну нулю J u(a) по a.

Ту саму формулу отримаємо, прирівнюючи нулю відцентровий момент інерції

.

Головними осями називають осі, щодо яких осьові моменти інерції набувають екстремальних значень, а відцентровий момент інерції дорівнює нулю.

Головних осей інерції можна провести безліч, взявши в якості початку координат будь-яку точку на площині. Для вирішення завдань опору матеріалів нас цікавлять лише Основні центральні осі інерції. Головні центральні осі інерціїпроходять через центр тяжкості перерізу.

Формула (3.17) дає два рішення, що відрізняються на 90°, тобто. дозволяє визначити два значення кута нахилу головних осей інерції щодо початкових осей. Щодо якої з осей виходить максимальний осьовий момент інерції J 1 = J max , а щодо якої – мінімальний J 2 = J min, доведеться вирішувати за змістом завдання.

Більше зручними виявляються інші формули, які однозначно визначають положення головних осей 1 і 2 (даються без висновку). При цьому позитивний кут відраховується від осі Оzпроти годинникової стрілки.

У формулі (3.19) знак "+" відповідає максимальному моменту інерції, а знак "-" мінімальному.

Зауваження . Якщо перетин має хоча б одну вісь симетрії, то щодо цієї осі та будь-якої іншої, їй перпендикулярної, відцентровий момент інерції дорівнює нулю.Відповідно до визначення головних осей інерції можна зробити висновок, що ці осі є головними осями інерції, тобто. вісь симетрії – завжди головна центральна вісь.

Для симетричних профілів, представлених у сортаменті, швелера або двотавра, головними центральними осями інерції будуть вертикальна та горизонтальна осі, що перетинаються на половині висоти профілю.