Якщо функція
диференційована в точці 
,
то її приріст можна у вигляді суми двох доданків
. Ці доданки є нескінченно малими функціями при 
. Перше доданок лінійно щодо 
,друге є нескінченно малою вищого порядку, ніж 
.Справді,
.
Таким чином другий доданок при 
швидше прагне до нуля та при знаходженні збільшення функції 
головну роль відіграє перший доданок 
або (оскільки 
)
.
Визначення
.
Головна частина збільшення функції
у точці 
, лінійна щодо
,називається диференціалом
функції
у цій точці і позначаєтьсяdyабоdf(x)
. (2)
Таким чином, можна зробити висновок: диференціал незалежної змінної збігається з її збільшенням, тобто 
.
Співвідношення (2) тепер набуває вигляду
(3)
Зауваження . Формулу (3) для стислості часто записують у вигляді
(4)
Геометричний зміст диференціала
Розглянемо графік диференційованої функції 
. Крапки 
іналежать графіку функції. У точці Мпроведена дотична Додо графіка функції, кут якої з позитивним напрямом осі 
позначимо через 
. Проведемо прямі MN
паралельно осі Ox
і 
паралельно осі Ой. Приріст функції дорівнює довжині відрізка 
. З прямокутного трикутника 
, в котрому 
, отримаємо
Викладені вище міркування дозволяють зробити висновок:
Диференціал функції
у точці 
зображується збільшенням ординати, що стосується графіка цієї функції у відповідній її точці. 
.
Зв'язок диференціалу з похідним
Розглянемо формулу (4)
.
Розділимо обидві частини цієї рівності на dxтоді
.
Таким чином, похідна функції дорівнює відношенню її диференціала до диференціалу незалежної змінної.
Часто це ставлення 
розглядається просто як символ, що означає похідну функції уза аргументом х.
Зручними позначеннями похідної є:
,
і так далі.
Використовуються також записи
,
,
особливо зручні, коли береться похідна від складного виразу.
2. Диференціал суми, твору та приватного.
Так як диференціал виходить з похідною множенням її на диференціал незалежної змінної, то, знаючи похідні основних елементарних функцій, а також правила для відшукання похідних, можна дійти аналогічних правил для відшукання диференціалів.
1 0 . Диференціал постійної дорівнює нулю
.
2 0 . Диференціал суми алгебри кінцевого числа диференційованих функцій дорівнює сумі алгебри диференціалів цих функцій
3 0 . Диференціал твору двох функцій, що диференціюються, дорівнює сумі творів першої функції на диференціал другої і другої функції на диференціал першої
.
Слідство. Постійний множник можна виносити за знак диференціалу
.
приклад. Знайти диференціал функції.
Рішення. Запишемо цю функцію у вигляді
,
тоді отримаємо
.
4. Функції, задані параметрично, їхнє диференціювання.
Визначення
.
Функція 
називається заданою параметрично, якщо обидві змінні х і
у
визначаються кожна окремо як однозначні функції від однієї й тієї ж допоміжної змінної – параметраt:
деtзмінюється в межах 
.
Зауваження
. Параметричне завдання функцій широко застосовується у теоретичній механіці, де параметр t
позначає час, а рівняння 
являють собою закони зміни проекцій точки, що рухається 
на осі 
і 
.
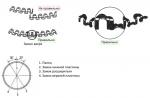
Зауваження . Наведемо параметричні рівняння кола та еліпса.
а) Коло з центром на початку координат та радіусом r має параметричні рівняння:
де 
.
б) Запишемо параметричні рівняння для еліпса:
де 
.
Виключивши параметр t з параметричних рівнянь розглянутих ліній, можна дійти їх канонічних рівнянь.
Теорема
. Якщо функція у від аргументу
х задана параметрично рівняннями 
, де 
і 
диференційовані поtфункції та 
, то
.
приклад. Знайти похідну функції увід х, заданою параметричними рівняннями
Рішення. 
.
24.1. Поняття диференціалу функції
Нехай функція у = ƒ (х) має в точці х відмінну від нуля похідну.
Тоді, за теоремою про зв'язок функції, її межі та нескінченно малої функції, можна записати D у/D х=ƒ"(х)+α, де α→0 при ∆х→0, або ∆у=ƒ"(х) ∆х+α ∆х.
Таким чином, збільшення функції ∆у являє собою суму двох доданків ƒ"(х) ∆х і а ∆х, які є нескінченно малими при ∆x→0. При цьому перший доданок є нескінченно мала функція одного порядку з ∆х, так як 
а другий доданок є нескінченно мала функція вищого порядку, ніж ∆х:
Тому перший доданок ƒ"(х) · ∆х називають головною частиною збільшенняфункції ∆у.
Диференціалом функціїу=ƒ(х) у точці х називається головна частина її збільшення, рівна добутку похідної функції на збільшення аргументу, і позначається dу (або dƒ(х)):
dy=ƒ"(х) ∆х. (24.1)
Диференціал dу називають також диференціалом першого порядку.Знайдемо диференціал незалежної змінної х, тобто диференціал функції у = х.
Так як у "=х" = 1, то, згідно з формулою (24.1), маємо dy = dx = ∆x, тобто диференціал незалежної змінної дорівнює приросту цієї змінної: dх = ∆х.
Тому формулу (24.1) можна записати так:
dy=ƒ"(х)dх, (24.2)
іншими словами, диференціал функції дорівнює добутку похідної цієї функції на диференціал незалежної змінної.
З формули (24.2) випливає рівність dy/dx=ƒ"(х). Тепер позначення
похідної dy/dx можна як ставлення диференціалів dy і dх.
<< Пример 24.1
Знайти диференціал функції ƒ(х)=3x 2 -sin(l+2x).
Рішення: За формулою dy=ƒ"(х) dx знаходимо
dy=(3х2-sin(l+2x))"dx=(6х-2cos(l+2х))dx.
<< Пример 24.2
Знайти диференціал функції
Обчислити dy при x=0, dx=0,1.
Рішення:
Підставивши х=0 та dx=0.1, отримаємо
24.2. Геометричний зміст диференціала функції
З'ясуємо геометричне значення диференціала.
Для цього проведемо до графіка функції у=ƒ(х) у точці М(х; у) дотичну МТ і розглянемо ординату цієї дотичної точки х+∆х (див. рис. 138). На малюнку ½ АМ½ = ∆х, | AM 1 | = ∆у. З прямокутного трикутника МАВ маємо:
Але, згідно з геометричним змістом похідної, tga=ƒ"(х). Тому АВ=ƒ"(х) ∆х.
Порівнюючи отриманий результат з формулою (24.1), отримуємо dy=АВ, тобто диференціал функції у=ƒ(х) у точці х дорівнює прирощенню ординати дотичної до графіка функції у цій точці, коли х отримає приріст ∆х.
У цьому полягає геометричний сенс диференціала.
24.3 Основні теореми про диференціали
Основні теореми про диференціали легко отримати, використовуючи зв'язок диференціала і похідної функції (dy=f"(x)dx) та відповідні теореми про похідні.
Наприклад, так як похідна функції у = дорівнює нулю, то диференціал постійної величини дорівнює нулю: dy = з "dx = 0 dx = 0".
Теорема 24.1.Диференціал суми, твору та частки двох диференційованих функцій визначаються такими формулами:
Доведемо, наприклад, другу формулу. За визначенням диференціалу маємо:
d(uv)=(uv)" dx=(uv" +vu" )dx=vu" dx+uv" dx=udv+vdu
Теорема 24.2.Диференціал складної функції дорівнює добутку похідної цієї функції за проміжним аргументом на диференціал цього проміжного аргументу.
Нехай у=ƒ(u) і u=φ(х) дві функції, що диференціюються, що утворюють складну функцію у=ƒ(φ(х)). За теоремою про похідну складну функцію можна написати
у "х = у" u u" x.
Помноживши обидві частини цієї рівності на dx, повчаємо у "х dx=у" u u" х dx. Але у" х dx=dy і u" х dx=du. Отже, останню рівність можна переписати так:
dy=у" u du.
Порівнюючи формули dy=у" х dx і dy=у" u du, бачимо, що перший диференціал функції у=ƒ(х) визначається однією і тією ж формулою незалежно від того, є її аргумент незалежною змінною або є функцією іншого аргументу.
Цю властивість диференціалу називають інваріантністю (незмінністю) форми першого диференціалу.
Формула dy=у" х dx на вигляд збігається з формулою dy=у" u du, але між ними є принципова відмінність: у першій формулі х - незалежна змінна, отже, dx=∆х, у другій формулі і є функція від х тому, взагалі кажучи, du≠∆u.
За допомогою визначення диференціалу та основних теорем про диференціали легко перетворити таблицю похідних у таблицю диференціалів.
Наприклад: d(cosu)=(cosu)" u du=-sinudu
24.4. Таблиця диференціалів
24.5. Застосування диференціала до наближених обчислень
Як вже відомо, збільшення ∆у функції у=ƒ(х) у точці х можна представити у вигляді ∆у=ƒ"(х) ∆х+α ∆х, де α→0 при ∆х→0, або ∆у= dy+α ∆х Відкидаючи нескінченно малу α ∆х вищого порядку, ніж ∆х, отримуємо наближену рівність
∆у≈dy, (24.3)
причому ця рівність тим точніша, чим менше ∆х.
Ця рівність дозволяє з великою точністю обчислити приблизно збільшення будь-якої диференційованої функції.
Диференціал зазвичай знаходиться значно простіше, ніж збільшення функції, тому формула (24.3) широко застосовується у обчислювальній практиці.
<< Пример 24.3
Знайти наближене значення збільшення функції у=х 3 -2х+1 при х=2 і ∆х=0,001.
Рішення: Застосовуємо формулу (24.3): ∆у≈dy=(х 3 -2х+1)" ∆х=(3х 2 -2) ∆х.
Отже, ∆у» 0,01.
Подивимося, яку похибку допустили, обчисливши диференціал функції замість її збільшення. Для цього знайдемо ∆у:
∆у=((х+∆х) 3 -2(х+∆х)+1)-(х 3 -2х+1)=х 3 +3х 2 ∆х+3х (∆х) 2 +(∆х ) 3 -2х-2 ∆х+1-х 3 +2х-1=∆х(3х 2 +3х ∆х+(∆х) 2 -2);
Абсолютна похибка наближення дорівнює
| ∆у-dy | = | 0,010006-0,011 = 0,000006.
Підставляючи в рівність (24.3) значення ∆у та dy, отримаємо
ƒ(х+∆х)-ƒ(х)≈ƒ"(х)∆х
ƒ(х+∆х)≈ƒ(х)+ƒ"(х) ∆х. (24.4)
Формула (24.4) використовується для обчислення наближених значень функцій.
<< Пример 24.4
Обчислити приблизно arctg(1,05).
Рішення: Розглянемо функцію ƒ(х)=arctgx. За формулою (24.4) маємо:
arctg(x+∆х)≈arctgx+(arctgx)" ∆х,
тобто. 
Так як х + ∆х = 1,05, то при х = 1 і ∆х = 0,05 отримуємо:
Можна показати, що абсолютна похибка формули (24.4) вбирається у величини М (∆х) 2 , де М - найбільше значення |ƒ"(х)| на сегменті [х;х+∆х].
<< Пример 24.5
Який шлях пройде тіло при вільному падінні на Місяці за 10,04 з початку падіння. Рівняння вільного падіння тіла
H = g л t 2/2, g л = 1,6 м/с 2 .
Рішення: Потрібно знайти H(10,04). Скористаємося наближеною формулою (ΔH≈dH)
H(t+∆t)≈H(t)+H"(t) ∆t. При t=10 с і ∆t=dt=0,04 с, H"(t)=g л t, знаходимо
Завдання (для самостійного вирішення).Тіло масою m=20 кг рухається зі швидкістю =10,02 м/с. Обчислити приблизно кінетичну енергію тіла
24.6. Диференціали вищих порядків
Нехай у = ƒ (х) диференційована функція, а її аргумент х - незалежна змінна.Тоді її перший диференціал dy=ƒ"(х)dx є також функція х; можна знайти диференціал цієї функції.
Диференціал від диференціала функції у = ƒ (х) називається її другим диференціалом(або диференціалом другого порядку) і позначається d 2 y або d 2 (х).
Отже, визначення d 2 y=d(dy). Знайдемо вираз другого диференціала функції у = ƒ (х).
Так як dx = ∆х не залежить від х, то при диференціюванні вважаємо dx постійним:
d 2 y=d(dy)=d(f"(x)dx)=(ƒ"(х)dx)" dx=f"(x)dx dx=f"(x)(dx) 2 тобто .
d 2 y=ƒ"(х)dх 2 . (24.5)
Тут dx 2 означає (dx) 2 .
Аналогічно визначається та знаходиться диференціал третього порядку
d 3 y = d (d 2 y) = d (ƒ "(х) dx 2) f" (x) (dx) 3 .
І, взагалі, диференціал n-го порядку є диференціал від диференціалу (n-1)-го порядку: dn y = d (dn-l y) = f (n) (x) (dx) n .
Звідси знаходимо, що, зокрема, при n=1,2,3
відповідно отримуємо:
тобто похідну функції можна розглядати як відношення її диференціалу відповідного порядку до відповідного ступеня диференціалу незалежної змінної.
Зазначимо, що це наведені вище формули справедливі лише, якщо х - незалежна змінна. Якщо ж функцію у = ƒ (х), де х - функція від будь-якої іншої незалежної змінної, то диференціали другого і вище порядків не мають властивість інваріантності форми і обчислюються за іншими формулами. Покажемо це з прикладу диференціала другого порядку.
Використовуючи формулу диференціала твору (d(uv)=vdu+udv), отримуємо:
d 2 y=d(f"(x)dx)=d(ƒ"(х))dx+ƒ"(х) d(dx)=ƒ"(х)dx dx+ƒ"(х) d 2 x , тобто.
d 2 y=ƒ"(х)dx 2 +ƒ"(х) d 2 x. (24.6)
Порівнюючи формули (24.5) і (24.6), переконуємося, що у разі складної функції формула диференціала другого порядку змінюється: з'являється другий доданок ƒ"(х) d 2 х.
Зрозуміло, що якщо х – незалежна змінна, то
d 2 x = d (dx) = d (l dx) = dx d (l) = dx 0 = 0
і формула (24.6) перетворюється на формулу (24.5).
<< Пример 24.6
Знайти d 2 y, якщо у = е 3х і х - незалежна змінна.
Рішення: Так як у "=3е 3х, у" = 9e 3х, то за формулою (24.5) маємо d 2 y = 9e 3x dx 2 .
<< Пример 24.7
Знайти d 2 y, якщо у = х 2 і х = t 3 +1і t-незалежна змінна.
Рішення: Використовуємо формулу (24.6): оскільки
у"=2х, у"=2, dx=3t 2 dt, d 2 x=6tdt 2
то d 2 y=2dx 2 +2x 6tdt 2 =2(3t 2 dt) 2 +2(t 3 +1)6tdt 2 =18t 4 dt 2 +12t 4 dt 2 +12tdt 2 =(30t 4 +12t)dt 2
Інше рішення: у = х 2, х = t 3 +1. Отже, у = (t 3 +1) 2 . Тоді за формулою (24.5)
d 2 у=у ¢¢ dt 2 ,
d 2 y = (30t 4 +12t) dt 2 .
Диференціаломфункції у=ƒ(х) у точці х називається головна частина її збільшення, рівна добутку похідної функції на збільшення аргументу, і позначається dу (або dƒ(х)): dy=ƒ"(х) ∆х.
Основні диференціали:
Диференціал функції має властивості, аналогічні властивостям похідної.
- Диференціал постійноїдорівнює нулю:
dc = 0, з = const. - Диференціал суми функцій, що диференціюютьсядорівнює сумі диференціалів доданків:
Слідство. Якщо дві функції, що диференціюються, відрізняються постійним доданком, то їх диференціали рівні
d(u+c) = du(c=const).
- Диференціал творудвох функцій, що диференціюються, дорівнює добутку першої функції на диференціал другий плюс добуток другий на диференціал першої:
d(uv) = udv + vdu.
Слідство. Постійний множник можна виносити за знак диференціалу
d(cu) = cdu (з = const).
- Диференціал приватного u/v двох функцій, що диференціюються і = і(х) і v = v(x) визначається формулою
- Властивість незалежності виду диференціала від вибору незалежної змінної (інваріантність форми диференціала): диференціал функції дорівнює добутку похідної на диференціал аргументу незалежного від того, чи є цей аргумент незалежною змінною або функцією іншої незалежної змінної.
Похідні та диференціали вищих порядків.
Нехай похідна деякою функцією fдиференційована. Тоді похідна від похідної цієї функції називається другий похіднийфункції fі позначається f". Таким чином,
f"(x) = (f"(x))" .
Якщо диференційована ( n- 1)-а похідна функції f, то її n-ї похідноїназивається похідна від ( n- 1)-ї похідної функції fі позначається f(n). Отже,
f(n)(x) = (f (n-1)(x))" , n ϵ N, f(0)(x) = f(x).
Число nназивається порядком похідної.
Диференціалом n-го порядкуфункції fназивається диференціал від диференціалу ( n- 1)-го порядку цієї функції. Таким чином,
d n f(x) = d(d n -1 f(x)), d 0 f(x) = f(x), n ϵ N.
Якщо x- незалежна змінна, то
dx= const та d 2 x = d 3 x = ... = d n x = 0.
І тут справедлива формула
d n f(x) = f (n) (x)(dx)n.
Похідні n-го порядку від основних елементарних функцій
Справедливі формули
Застосування похідних для вивчення функцій.
Основні теореми диференціювання функцій:
Теорема Роля
Нехай функція f: [a, b] → Rбезперервна на сегменті [ a, b], і має кінцеву або нескінченну похідну усередині цього сегмента. Нехай, крім того, f(a) = f(b). Тоді всередині сегмента [ a, b] знайдеться точка ξ така, що f"(ξ ) = 0.
Теорема Лагранжа
Якщо функція f: [a, b] → Rбезперервна на сегменті [ a, b] і має кінцеву або нескінченну похідну у внутрішніх точках цього сегмента, таке, що f(b) - f(a) = f"(ξ )(b - a).
Теорема Коші
Якщо кожна з функцій fі gбезперервна на [ a, b] і має кінцеву або нескінченну похідну на ] a, b[і якщо, крім того, похідна g"(x) ≠ 0 на ] a, b[, то таке, що справедлива формула
Якщо додатково зажадати, щоб g(a) ≠ g(b), то умова g"(x) ≠ 0 можна замінити менш жорстким:
Будучи нерозривно пов'язаними між собою, вони вже кілька століть активно використовуються при вирішенні практично всіх завдань, які виникали в процесі науково-технічної діяльності людини.
Виникнення поняття про диференціал
Вперше роз'яснив, що таке диференціал, один із творців (поряд з Ісааком Ньютоном) диференціального числення знаменитий німецький математик Готфрід Вільгельм Лейбніц. До цього математиками 17 ст. використовувалося дуже нечітке і розпливчасте уявлення про деяку нескінченно малу «неподільну» частину будь-якої відомої функції, що представляла дуже малу постійну величину, але не рівну нулю, менше якої значення функції бути просто не можуть. Звідси був лише один крок до введення уявлення про нескінченно малі прирощення аргументів функцій і відповідні їм прирощення самих функцій, що виражаються через похідні останніх. І цей крок було зроблено практично одночасно двома вищезгаданими великими вченими.
Виходячи з необхідності вирішення нагальних практичних завдань механіки, які ставила перед наукою бурхливо розвивається промисловість і техніка, Ньютон і Лейбніц створили загальні способи знаходження швидкості зміни функцій (насамперед стосовно механічної швидкості руху тіла за відомою траєкторією), що призвело до введення таких понять, як похідна та диференціал функції, а також знайшли алгоритм вирішення зворотного завдання, як за відомою (змінною) швидкістю знайти пройдений шлях, що призвело до появи поняття інтеграла.
У працях Лейбніца і Ньютона вперше з'явилося уявлення у тому, що диференціали - це пропорційні приростам аргументів Δх основні частини прирощень функцій Δу, які можуть бути успішно застосовані до обчислення значень останніх. Інакше кажучи, ними було відкрито, що збільшення функції може бути в будь-якій точці (всередині області її визначення) виражено через її похідну як Δу = y"(x) Δх + αΔх, де α Δх - залишковий член, що прагне до нуля при Δх→ 0, набагато швидше, ніж саме Δх.
Згідно з основоположниками матаналізу, диференціали - це якраз і є перші члени у виразах прирощень будь-яких функцій. Ще не маючи чітко сформульованого поняття межі послідовностей, вони інтуїтивно зрозуміли, що величина диференціала прагне похідної функції при Δх→0 - Δу/Δх→ y"(x).
На відміну від Ньютона, який був насамперед фізиком, і розглядав математичний апарат як допоміжний інструмент дослідження фізичних завдань, Лейбніц приділяв більшу увагу самому цьому інструментарію, включаючи систему наочних і зрозумілих позначень математичних величин. Саме він запропонував загальноприйняті позначення диференціалів функції dy=y"(x)dx, аргументу dx та похідної функції у вигляді їх відношення y"(x)=dy/dx.
Сучасне визначення
Що таке диференціал із погляду сучасної математики? Він був із поняттям збільшення змінної величини. Якщо змінна y приймає спочатку значення y = y 1 , а потім y = y 2 то різниця y 2 ─ y 1 називається збільшенням величини y.
Приріст може бути позитивним. негативним та рівним нулю. Слово «прирощення» позначається Δ, запис Δу (читається «дельта ігрок») позначає збільшення величини y. отже Δу = y 2 ─ y 1 .
Якщо величину Δу довільної функції y = f (x) можливо представити у вигляді Δу = A Δх + α, де A немає залежності від Δх, тобто A = const при даному х, а доданок α при Δх→0 прагне до йому ще швидше, ніж саме Δх, тоді перший («головний») член, пропорційний Δх, і є для y = f (x) диференціалом, що позначається dy або df(x) (читається «де игрек», «де еф від ікс »). Тому диференціали - це «головні» лінійні щодо Δх складові прирощень функцій.
Механічне тлумачення
Нехай s = f(t) - відстань прямолінійно рухається від початкового положення (t - час перебування в дорозі). Приріст Δs - це шлях точки за інтервал часу Δt, а диференціал ds = f" (t) Δt - це шлях, який точка пройшла б за той же час Δt, якби вона зберегла швидкість f"(t), досягнуту до моменту t . При нескінченно малому Δt уявний шлях ds відрізняється від істинного Δs на нескінченно малу величину, що має вищий порядок щодо Δt. Якщо швидкість момент t не дорівнює нулю, то ds дає наближену величину малого зміщення точки.
Геометрична інтерпретація
Нехай лінія L є графіком y = f(x). Тоді Δ х= MQ, Δу = QM" (див. рисунок нижче). Дотична MN розбиває відрізок Δу на дві частини, QN і NM". Перша пропорційна Δх і дорівнює QN = MQ∙tg (кута QMN) = Δх f "(x), тобто QN є диференціал dy.
Друга частина NM" дає різницю Δу ─ dy, при Δх→0 довжина NM" зменшується ще швидше, ніж збільшення аргументу, тобто у неї порядок трохи вище, ніж у Δх. У даному випадку, при f "(x) ≠ 0 (дотична не паралельна ОХ), відрізки QM" і QN еквівалентні; іншими словами NM" зменшується швидше (порядок трохи її вище), ніж повне збільшення Δу = QM". Це видно на малюнку (з наближенням M" до М відрізок NM" становить все менший відсоток відрізка QM").
Отже, графічно диференціал довільної функції дорівнює величині збільшення ординати її дотичної.
Похідна та диференціал
Коефіцієнт A у першому доданку виразу прирощення функції дорівнює величині її похідної f "(x). Таким чином, має місце наступне співвідношення - dy = f "(x)Δх, або df (x) = f "(x)Δх.
Відомо, що збільшення незалежного аргументу дорівнює його диференціалу х = dx. Відповідно, можна написати: f"(x) dx = dy.
Знаходження (іноді кажуть, «рішення») диференціалів виконується за тими самими правилами, що й для похідних. Перелік їх наведено нижче.
Що універсальніше: збільшення аргументу чи його диференціал
Тут потрібно зробити деякі пояснення. Подання величиною f"(x)Δх диференціала можливе при розгляді х як аргумент. Але функція може бути складною, в якій х може бути функцією деякого аргументу t. Тоді подання диференціала виразом f"(x)Δх, як правило, неможливо; окрім випадку лінійної залежності х = at + b.
Що ж до формули f "(x)dx= dy, то й у разі незалежного аргументу х (тоді dx = Δх), і у разі параметричної залежності х від t, вона представляє диференціал.
Наприклад, вираз 2 x Δх представляє для y = x 2 її диференціал, коли є аргумент. Покладемо тепер х = t 2 і вважатимемо t аргументом. Тоді y = x2 = t4.
Цей вираз не пропорційний Δt і тому тепер 2xΔх не є диференціалом. Його можна знайти з рівняння y = x2 = t4. Він виявляється дорівнює dy=4t 3 Δt.
Якщо ж взяти вираз 2xdx, воно представляє диференціал y = x 2 при будь-якому аргументі t. Дійсно, при х = t2 отримаємо dx = 2tΔt.
Значить 2xdx = 2t 2 2tΔt = 4t 3 Δt, тобто вирази диференціалів, записані через дві різні змінні, збіглися.
Заміна прирощень диференціалами
Якщо f "(x) ≠ 0, то Δу та dy еквівалентні (при Δх→0); при f "(x) = 0 (що означає і dy = 0), вони не еквівалентні.
Наприклад, якщо y = x 2 то Δу = (x + Δх) 2 ─ x 2 = 2xΔх + Δх 2 , а dy = 2xΔх. Якщо х=3, то маємо Δу = 6Δх + Δх 2 та dy = 6Δх, які еквівалентні внаслідок Δх 2 →0, при х=0 величини Δу = Δх 2 та dy=0 не еквівалентні.
Цей факт, разом із простою структурою диференціала (тобто лінійності по відношенню до Δх), часто використовується в наближених обчисленнях, припущення, що Δу ≈ dy для малих Δх. Знайти диференціал функції, як правило, легше, ніж обчислити точне значення збільшення.
Наприклад, маємо металевий куб із ребром х=10,00 см. При нагріванні ребро подовжилося на Δх = 0,001 см. Наскільки збільшився об'єм V куба? Маємо V = х 2 так що dV = 3x 2 Δх = 3∙10 2 ∙0/01 = 3 (см 3). Збільшення обсягу ΔV еквівалентно диференціалу dV, так що ΔV = 3 см 3 . Повне обчислення дало б V =10,01 3 ─ 10 3 = 3,003001. Але в цьому результаті всі цифри, крім першої, ненадійні; отже, однаково, потрібно округлити його до 3 см 3 .
Очевидно, що такий підхід є корисним, тільки якщо можливо оцінити величину помилки, що привноситься при цьому.
Диференціал функції: приклади
Спробуємо знайти диференціал функції y = x3, не знаходячи похідної. Дамо аргументу збільшення і визначимо Δу.
Δу = (Δх + x) 3 ─ x 3 = 3x 2 Δх + (3xΔх 2 + Δх 3).
Тут коефіцієнт A = 3x 2 не залежить від Δх, так що перший член пропорційний Δх, інший член 3xΔх 2 + Δх 3 при Δх→0 зменшується швидше, ніж приріст аргументу. Отже, член 3x 2 Δх є диференціал y = x 3:
dy=3x 2 Δх=3x 2 dx або d(x 3) = 3x 2 dx.
У цьому d(x 3) / dx = 3x 2 .
Знайдемо тепер dy функції y = 1/x через її похідну. Тоді d(1/x) / dx = ─1/х2. Тому dy = ─ Δх/х2.
Диференціали основних функцій алгебри наведені нижче.
Наближені обчислення із застосуванням диференціалу
Обчислити функцію f(x), а також її похідну f"(x) при x=a часто неважко, а ось зробити те ж саме на околиці точки x=a буває нелегко. Тоді на допомогу приходить наближений вираз
f(a + Δх) ≈ f "(a)Δх + f(a).
Воно дає наближене значення функції при малих збільшеннях через її диференціал f "(a)Δх.
Отже, дана формула дає наближений вираз для функції кінцевої точки деякої ділянки довжиною Δх у вигляді суми її значення в початковій точці цієї ділянки (x=a) і диференціала в тій же початковій точці. Похибка такого способу визначення значення функції ілюструє рисунок нижче.
Однак відомий і точний вираз значення функції для x=a+Δх, що дається формулою кінцевих прирощень (або, інакше, формулою Лагранжа)
f(a+ Δх) ≈ f "(ξ) Δх + f(a),
де точка x = a+ ξ знаходиться на відрізку від x = a до x = a + Δх, хоча точне положення її невідоме. Точна формула дозволяє оцінювати похибку наближеної формули. Якщо ж у формулі Лагранжа покласти ξ = Δх /2, то хоч вона і перестає бути точною, але дає, як правило, набагато краще наближення, ніж вихідний вираз через диференціал.
Оцінка похибки формул за допомогою диференціала
У принципі неточні, і привносять у дані вимірів відповідні помилки. Їх характеризують граничною чи, коротше, граничною похибкою - позитивним числом, явно перевищує цю помилку за абсолютною величиною (чи крайньому разі рівним їй). Граничною називають частки від її поділу на абсолютне значення виміряної величини.
Нехай точна формула y=f(x) використана для обчислення функції y, але значення x є результатом вимірювання і тому привносить у y помилку. Тоді, щоб знайти граничну абсолютну похибку │Δу│функції y використовують формулу
│Δу│≈│dy│=│ f "(x)││Δх│,
де │Δх│ є граничною похибкою аргументу. Величину │Δу│ слід округлити у бік збільшення, т.к. неточною є сама заміна обчислення збільшення обчислення диференціала.
