A physical pendulum is a rigid body that can swing around a fixed axis. Consider small oscillations of the pendulum. The position of the body at any moment of time can be characterized by the angle of its deviation from the equilibrium position (Fig. 2.1).
Let us write the equation of moments about the axis of rotation OZ (axis OZ passes through the suspension point O perpendicular to the plane of the figure "from us"), neglecting the moment of friction forces if the moment of inertia of the body is known
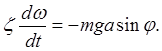
Here is the moment of inertia of the pendulum about the axis OZ,
The angular velocity of the pendulum,
M z =- - the moment of gravity relative to the OZ axis,
a is the distance from the center of gravity of the body C to the axis of rotation.
If we assume that during rotation, for example, counterclockwise, the angle increases, then the moment of gravity causes a decrease in this angle and, therefore, at the moment M z<0. Это и отражает знак минус в правой части (1)
Considering that and, taking into account the smallness of oscillations, we rewrite equation (1) in the form:
(we took into account that for small fluctuations, where the angle is expressed in radians). Equation (2) describes harmonic oscillations with a cyclic frequency and period
A special case of a physical pendulum is a mathematical pendulum. The entire mass of the mathematical pendulum is practically concentrated at one point - the center of inertia of the pendulum C. An example of a mathematical pendulum is a small massive ball suspended on a long light inextensible thread. In the case of a mathematical pendulum, a = l, where l is the length of the thread, and formula (3) goes into the well-known formula
Comparing formulas (3) and (4), we conclude that the period of oscillation of a physical pendulum is equal to the period of oscillation of a mathematical pendulum with length l, called the reduced length of the physical pendulum:
The period of oscillation of a physical pendulum (and, consequently, its reduced length) nonmonotonically depends on the distance. This is easy to see if, in accordance with the Huygens-Steiner theorem, the moment of inertia is expressed in terms of the moment of inertia about a parallel horizontal axis passing through the center of mass: Then the oscillation period will be equal to:
The change in the oscillation period when the axis of rotation is removed from the center of mass O in both directions by a distance a is shown in Fig. 2.2.
> Kinematics of pendulum oscillations
A pendulum is any body suspended so that its center of gravity is below the point of suspension. A hammer hanging on a nail, scales, a load on a rope - all these are oscillatory systems, similar to the pendulum of a wall clock (Fig. 2.3).
Any system capable of performing free oscillations has a stable equilibrium position. For a pendulum, this is the position in which the center of gravity is on the vertical below the suspension point. If we take the pendulum out of this position or push it, then it will begin to oscillate, deviating either in one direction or the other from the equilibrium position. The largest deviation from the equilibrium position, to which the pendulum reaches, is called the amplitude of oscillation. The amplitude is determined by the initial deflection or push with which the pendulum was set in motion. This property - the dependence of the amplitude on the conditions at the beginning of the movement - is characteristic not only for the free oscillations of the pendulum, but also in general for the free oscillations of very many oscillatory systems.
If we attach a hair to the pendulum - a piece of thin wire or an elastic nylon thread - and we move a smoked glass plate under this hair, as shown in fig. 2.3. If you move the plate with constant speed in the direction perpendicular to the plane of oscillation, then the hair will draw a wavy line on the plate (Fig. 2.4). In this experiment, we have the simplest oscilloscope - this is the name of the instruments for recording oscillations. The traces that an oscilloscope records are called waveforms. Thus, fig. 2.2.3. is an oscillogram of pendulum oscillations. The oscillation amplitude is depicted on this oscillogram by the segment AB, which gives the greatest deviation of the wavy curve from the straight line ab, which the hair would draw on the plate with a stationary pendulum (resting in equilibrium). The period is represented by a segment CD, equal to the distance that the plate moves during the period of the pendulum.
Recording the oscillations of a pendulum on a sooty plate
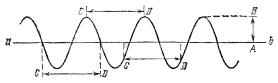
Oscillogram of pendulum oscillations: AB - amplitude, CD - period
Since we are moving the smoked plate uniformly, any movement of it is proportional to the time during which it took place. We can therefore say that along the straight line ab, on a certain scale (depending on the speed of the plate), time is plotted. On the other hand, in the direction perpendicular to ab, the hair marks on the plate the distances of the end of the pendulum from its equilibrium position, i.e. the distance traveled by the end of the pendulum from this position. Thus, an oscillogram is nothing more than a graph of movement - a graph of path versus time.
As we know, the slope of the line on such a graph represents the speed of movement. The pendulum passes through the equilibrium position with top speed. Accordingly, the slope of the wavy line in Fig. 2.2.3. greatest at those points where it intersects the line ab. On the contrary, at the moments of the greatest deviations the speed of the pendulum is equal to zero. Accordingly, the wavy line in Fig. 4 at those points where it is farthest from ab has a tangent parallel to ab, i.e., a slope equal to zero.
A physical pendulum is a rigid body that is in the field of gravity and has a horizontal axis of rotation that does not pass through the center of gravity of the body.
Let - the mass of the body, J - its moment of inertia about the axis of rotation - the distance from the center of gravity to the axis of rotation (Fig. 36). Removed from the equilibrium position, the body will rotate or oscillate. In both cases, the differential equation of motion has the same form (we neglect the friction forces):
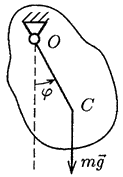
Let the initial conditions be such that the angle remains small all the time (the maximum deviation from the vertical does not exceed ). Then we can approximately accept (in radians) and consider a simpler equation:
or, which is the same, the equation
This equation is called the differential equation of small oscillations of a physical pendulum. It follows from it that small oscillations of the physical pendulum are harmonic oscillations of the frequency
and period
The amplitude and phase of the oscillations will be determined by the initial deviation and the initial angular velocity of the physical pendulum.
Questions for self-examination
1. What is called the moment of momentum of a material point?
2. What is called the kinetic moment of a mechanical system relative to a given center, a given axis?
3. Give general formulas for determining the kinetic moment of a mechanical system (relative to a given center, a given axis).
4. Give the mathematical notation of the theorem on the change in angular momentum. Give a verbal formulation of the theorem.
5. In what cases does the angular momentum of the system or its projection onto the axis remain constant during the motion of the system?
6. What coordinate axes are called Koenig's axes?
7. Lead general formula to determine the angular momentum of a rigid body relative to a given fixed center?
8. How is the angular momentum of a body calculated during its translational and rotational movements?
9. How are the differential equations of motion of a body when it forward movement? When rotating around a fixed axis? With plane-parallel motion?
10. What is called a physical pendulum? How is the period of its small oscillations determined?
Exercises
1. A material point M of the mass moves along a circle of radius R according to the equation (Fig. 37). Calculate and plot the momentum and moment of momentum of a point at .
STUDY OF FREE OSCILLATIONS OF A PHYSICAL PENDULUM
Goal of the work. Determination of the moment of inertia of a physical pendulum by two methods, measuring: 1) the period of its small oscillations; 2) its reduced length.
Introduction
A physical pendulum is any rigid body that oscillates under the action of gravity around a horizontal axis that does not pass through the center of inertia of the body. It is always possible to choose a mathematical pendulum that is synchronous with a given physical one, i.e. such a mathematical pendulum whose period of oscillation is equal to the period of oscillation of a physical pendulum. The length of such a mathematical pendulum is called reduced length physical pendulum .
Let us derive the formula for the oscillation period of a physical pendulum. On fig. 1 point ABOUT- trace of the horizontal axis of rotation, point IN- center of gravity. It should be noted that in a uniform gravity field, the center of inertia and the center of gravity coincide.
The body oscillates under the action of a torque:
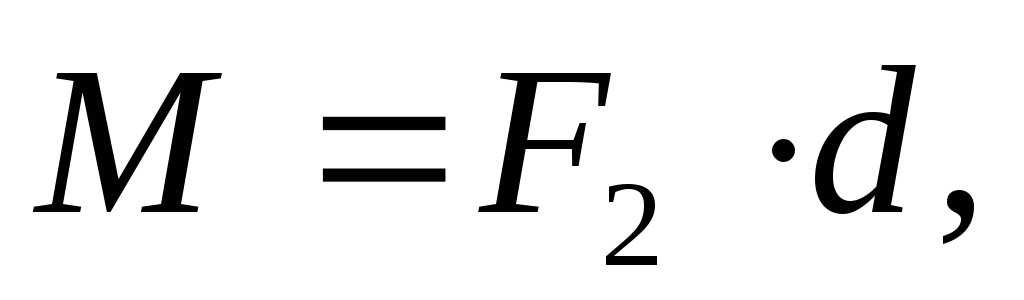(1)
Where 
- distance from the axis of rotation to the center of gravity of the body, equal to OV.
From figure 1 it follows that
Here φ
- angular displacement of the body, counted from the equilibrium position. For small values φ
angular displacement can be considered as a vector lying on the axis of rotation, the direction of which is determined by the direction of rotation of the body from the equilibrium position to the given direction by the rule of the right screw. Given that the vectors 
And 
anti-parallel, follows the magnitudes of the projections M And φ
assign opposite signs to the axis of rotation.
Then formula (1) takes the form
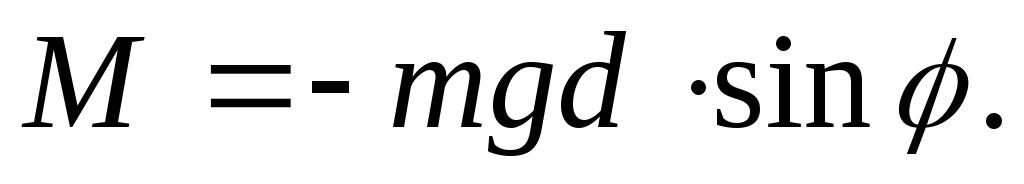(1a)
At small angles φ we can confine ourselves to the first term of the expansion of the function sinφ in a row
and accept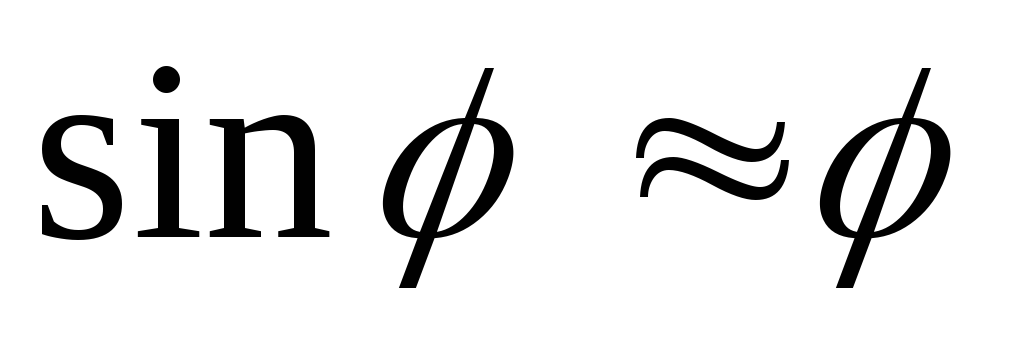 
, If φ
expressed in radians. Then formula (1a) can be written as follows:
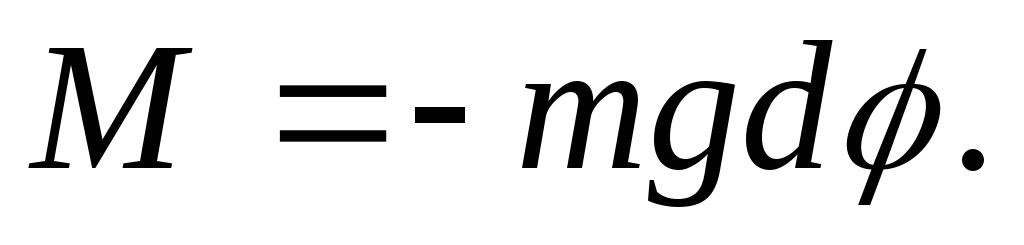(2)
We use the basic law of the dynamics of rotational motion, writing it in projections onto the axis of rotation:
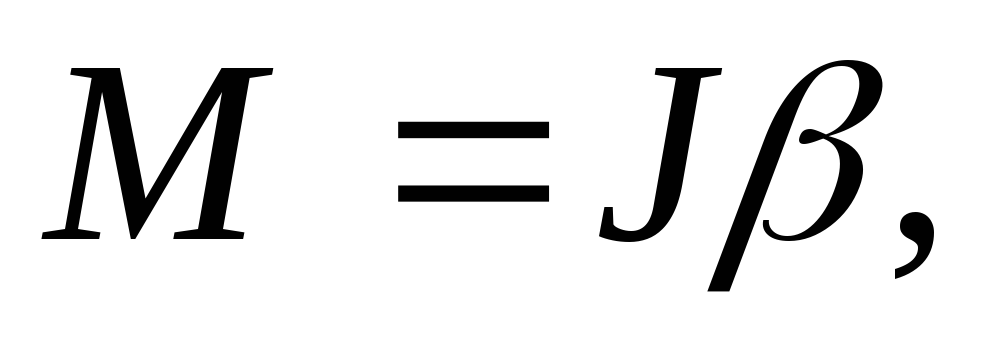(3)
Where 
- the moment of inertia of the body about the axis of rotation;
- angular acceleration, and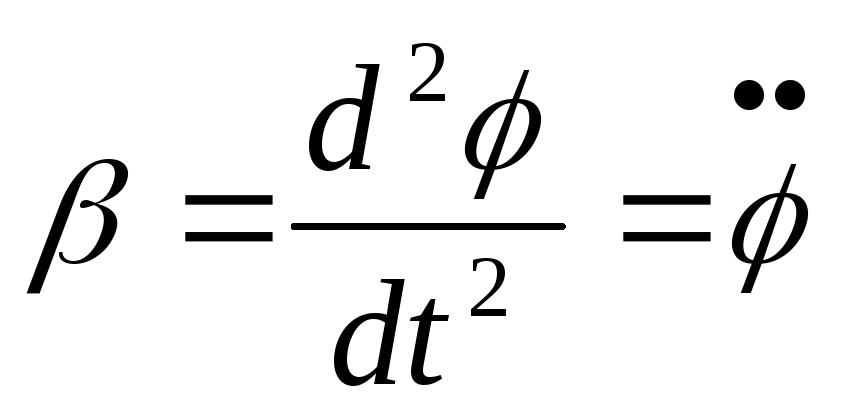 
.
Substituting into formula (3) the moment of force from formula (2), we obtain
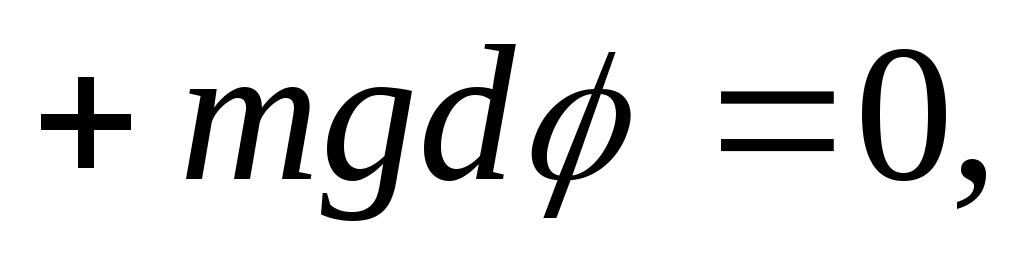
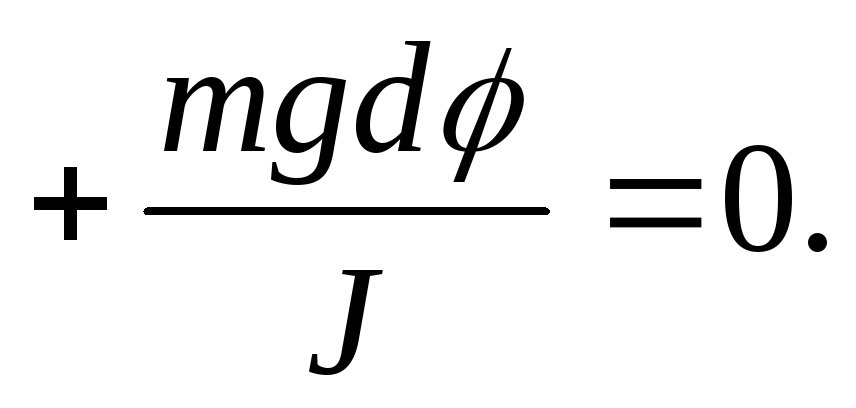(4)
This second-order linear homogeneous differential equation with constant coefficients is known to have a solution
φ(t) = φ 0 cos(ωt + α ), (5)
containing two arbitrary constants φ 0 And α determined by the initial conditions. Quantities φ 0 And α are called, respectively, the amplitude and the initial phase of the oscillations. Note that the cyclic frequency ω , as well as the oscillation period T f, is determined by the dynamic properties of the system and are, respectively,
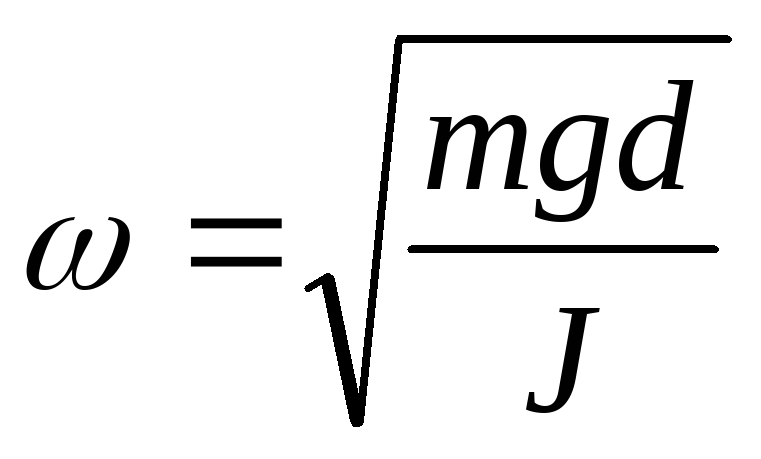And 
(6)
which can be verified by substituting the solution φ(t) in the form of formula (5) into equation (4).
It is known that the period of oscillation of a mathematical pendulum is equal to
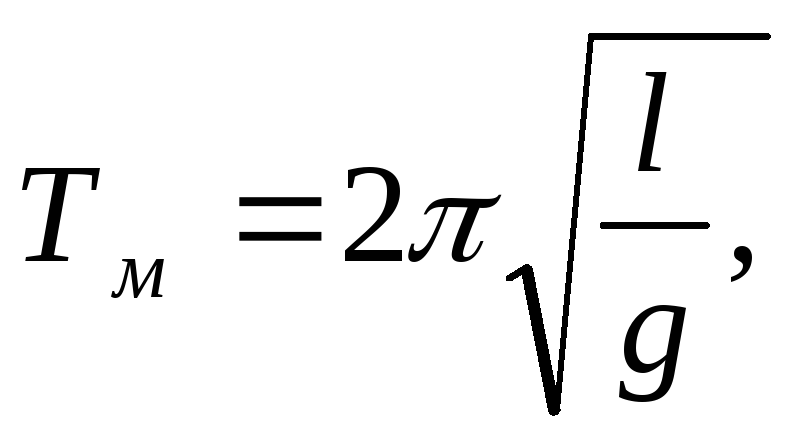
whence it follows that a mathematical pendulum will have the same period of oscillation as a given physical one, if its length is equal to
(7)
This is the formula for the reduced length of a physical pendulum.
Description of the installation and measurement methods
Installation includes: base, a vertical post, mathematical and physical pendulums with suspension units on the upper bracket, a bracket for installing a photo sensor, a photo sensor for recording the oscillation period of the physical and mathematical pendulums; electronic control unit including oscillation counter and stopwatch.
The base is equipped with three adjustable feet and a clamp for fixing the vertical stand.
The vertical stand is made of a metal tube, on which a millimeter scale is applied.
The mathematical pendulum has a bifilar suspension made of a nylon thread, on which a weight in the form of a metal ball is suspended, and a device for changing the length of the pendulum suspension.
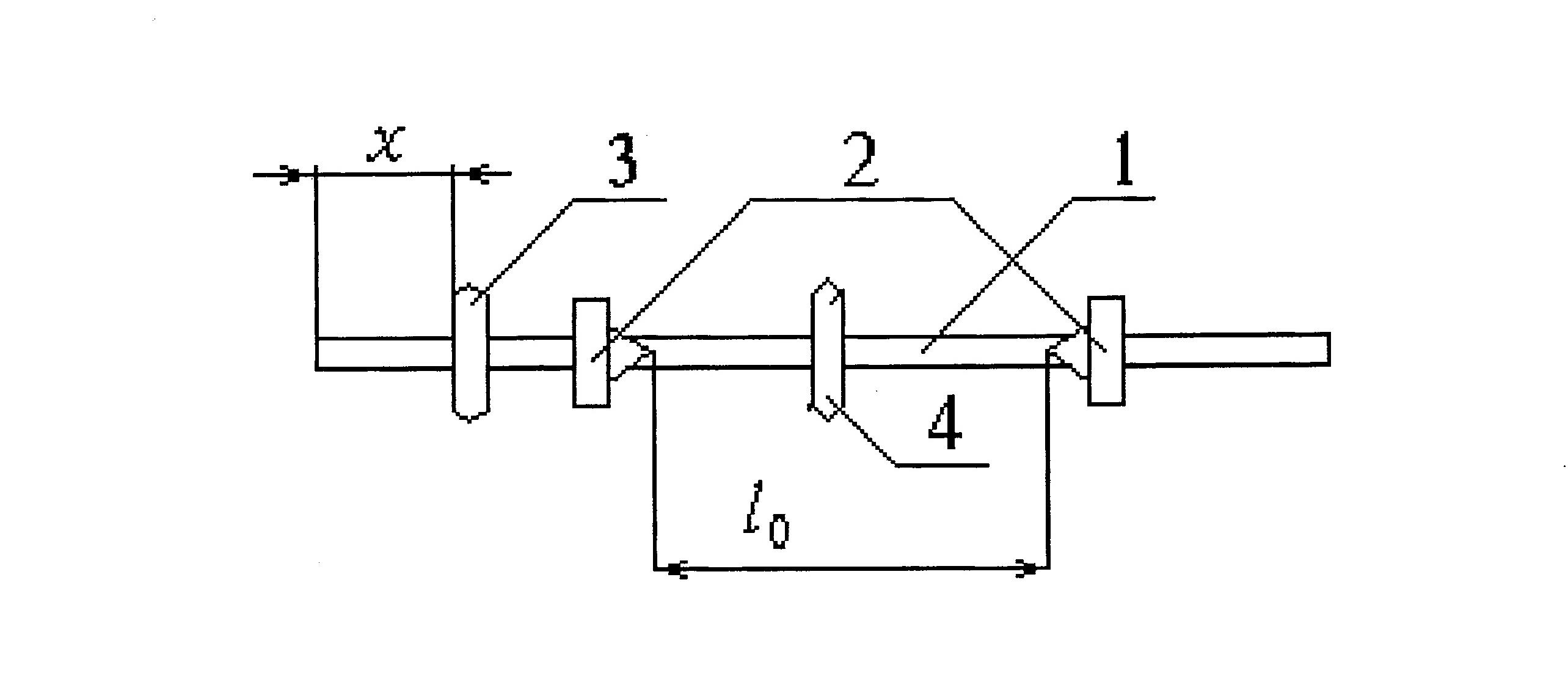
The physical pendulum (Fig. 2) has a rigid metal rod 1 with risks every 10 mm for measuring the length, two prismatic supports 2, which are installed in the working position on the V-shaped supports of the tripod, two weights 3 and 4 with the ability to move and fix along the entire length of the rod. The position of the fixed weight 4 is chosen so that with the help of the adjusting weight 3, shifting it a distance X, it was possible to achieve equality T 1 And T 2 in the forward and reverse positions of the pendulum.
Distance between reference prisms l 0 = 245 mm. The mass of the physical pendulum is 0.8329 kg.
The suspension units of the mathematical and physical pendulums are located on diametrically opposite sides of the bracket relative to the vertical post.
The bracket has a clamp for mounting on a vertical stand and elements for fixing the photosensor.
Installation works from the electronic block FM 1/1.
When taking measurements, a vernier caliper and a balancing prism are used.
One of the methods for determining the moment of inertia of the pendulum about the axis passing through the reference prism is to determine the period of oscillation T pendulum about this axis, mass m and distance d from the center of gravity to the axis (see formula (6) for T f). In this case, the moment of inertia of the pendulum is calculated by the formula
(8)
The position of the center of gravity is determined using a balancing prism.
In addition to this method, in practice, the method of determining the moment of inertia from the reduced length of a physical pendulum is often used. The reduced length is found from experience by selecting a mathematical pendulum that oscillates synchronously with a given physical pendulum. Having determined the length of the mathematical pendulum l P and measuring m And d, find the moment of inertia by the formula
(9)
Work order
First method
1. Turn on the electronic stopwatch. Press the "RESET" button. Hanging the pendulum on prism 2 (see Fig. 2), deflect it at a small angle (5-6 degrees), press the "START" button, release the pendulum without a push and fix: with a counter 10 oscillations (left panel), with a stopwatch, the time of these oscillations (right board). Take measurements five times. Then make similar measurements, hanging the pendulum on the opposite prism 2. Enter the data in table 1. Calculate t Wed, and then find the oscillation period using the formula
Record the result in table 1.
2. To determine the distance d from the center of gravity to the axis of rotation, remove the pendulum from the support and put it on a special stand (balancing prism). On a stand that has a sharp edge, the pendulum must be balanced. Measure the distance from the point located above the face of the balancing prism to the reference prism with a scale bar with an accuracy of 1 mm. Then calculate the moment of inertia using formula (8). Record the result in table 3.
Second method
By changing the length of the mathematical pendulum, ensure that it oscillates synchronously with the physical one. Complete coincidence of the periods of both pendulums is not easy to achieve. Therefore, it follows, by gradually changing the length of the thread of the mathematical pendulum, to achieve this. So that the pendulums oscillate synchronously for 10 oscillations. Measure the distance from the ball to the suspension point. pendulum length l equal to this distance plus the radius of the ball. It can be considered as the reduced length l P physical pendulum. The length of a mathematical pendulum oscillating synchronously with a given physical pendulum should be selected at least five times and found l n wed. Enter the results in Table 2. Calculate the moment of inertia using formula (9) and enter the measurement result in Table 3. Repeat similar measurements and calculations by hanging the pendulum on the second prism.
Table 1
|
Rotation axis position |
Distance from the axis of rotation to the center of gravity, m |
Time of 10 oscillations, s |
Average value of the oscillation period T Wed, With |
|||||
|
t 1 |
t 2 |
t 3 |
t 4 |
t 5 |
t Wed |
|||
table 2
|
ball radius r, m |
l P , m |
l n wed, m |
||||
Table 3
Processing of measurement results
1. Calculate the measurement error of the moment of inertia in accordance with the rules set forth in the guidelines. To do this, calculate the marginal error in determining the moment of inertia using the oscillation method using the formula
When determining the time t And l P random errors can be large. Random error Δt calculate by formula
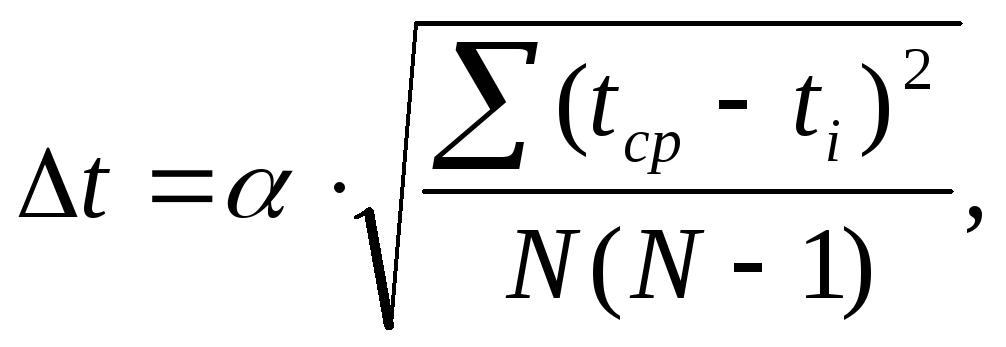
Where N is the number of measurements. For reliability, 0.95 and N= 5 (in our case), α = 2.8. The resulting random error is compared with the instrumental error equal to the stopwatch division value, i.e. 0.001 s In calculations, a larger error should be used, taking it as the marginal error in determining the time. Similarly, the error in the definition is calculated l P .
Values g And π
known with greater accuracy, so the relative errors,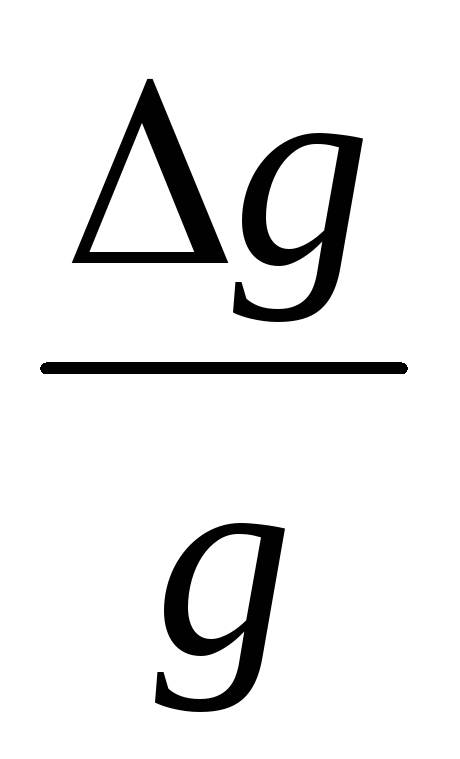 
And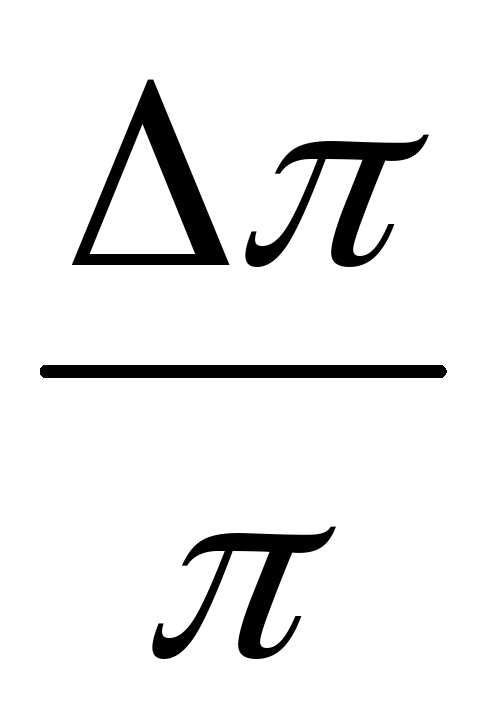 
can be made almost arbitrarily small. In order not to aggravate measurement errors with calculation errors, the values g And π
it is enough to take with so many decimal places so that 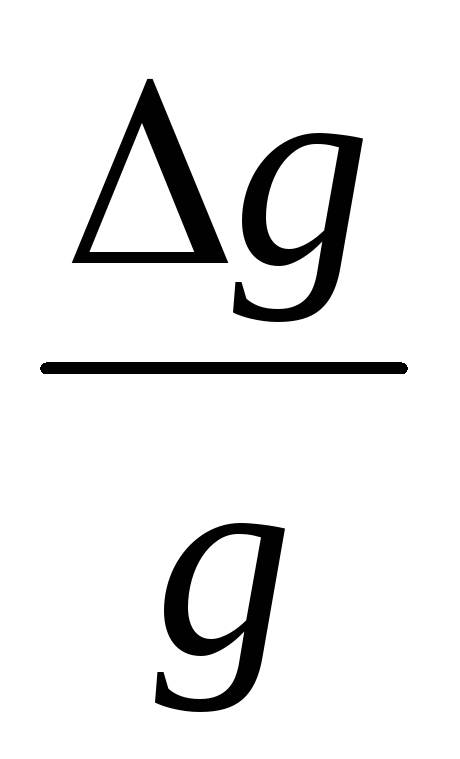And 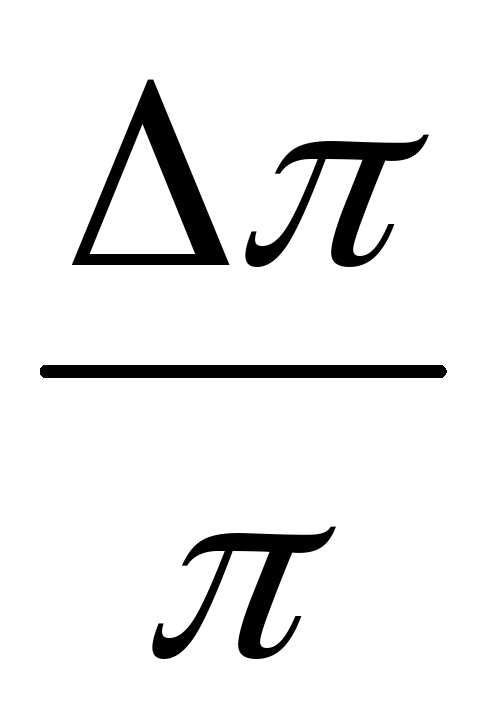were an order of magnitude smaller than the largest of the values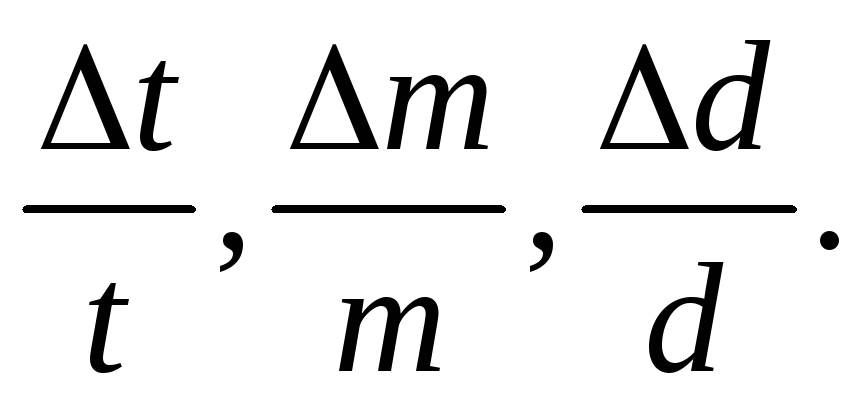 
2. According to the calculated relative error 
find absolute error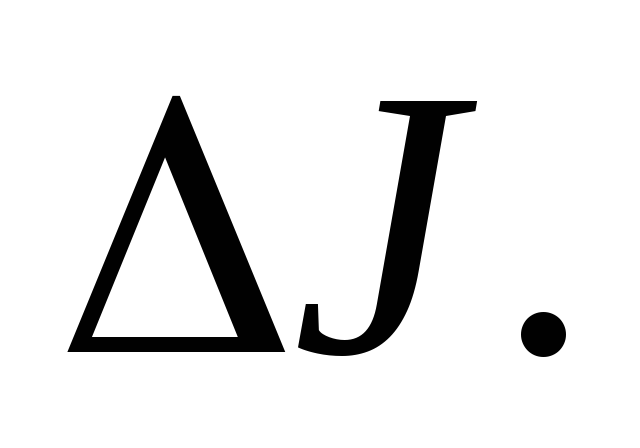 
3. Present the results of measurements of the moment of inertia in the form
CONTROL QUESTIONS
Define harmonic vibrations.
What is called a mathematical pendulum?
What is the reduced length of a physical pendulum called?
How is the formula for the period of oscillation of a physical pendulum derived?
LITERATURE
Trofimova T.K. Physics course. M., 2000.
Guidelines for laboratory work in physics (works 60 - 63), MIIT. 1976.
DEFINITION: physical pendulum we will call a rigid body capable of oscillating around a fixed axis that does not pass (not coincide) through its center of inertia.
When the pendulum deviates from the equilibrium position by an angle j, a torque arises that tends to return the pendulum to the equilibrium position (Fig. 8.8).
This moment is
where m is the mass of the pendulum; l is the distance from the suspension point "O" to the center of inertia of the pendulum "C".
Let's denote J - the moment of inertia of the pendulum about the axis passing through the suspension point, then . In the case of small oscillations, we obtain the equation
,
Where . It follows that for small deviations from the equilibrium position, the physical pendulum performs harmonic oscillations, the frequency of which depends on the mass of the pendulum, the moment of inertia of the pendulum relative to the axis of rotation, and the distance between the axis of rotation and the center of inertia of the pendulum.
The oscillation period of a physical pendulum will be determined by the expression:
. (8.14)
Comparing this expression with the period of oscillation of a mathematical pendulum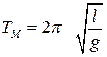 
we get that a mathematical pendulum with length 
will have the same oscillation period as the given physical pendulum. This value is called reduced length physical pendulum.
DEFINITION: Reduced length of a physical pendulum is the length of such a mathematical pendulum, the period of oscillation of which coincides with the period of oscillation of a given physical pendulum.
All topics in this section:
A few introductory remarks about the subject of physics.
The world surrounding us is material: it consists of eternally existing and continuously moving matter. Matter in the broadest sense of the word is everything that really exists in nature and m
Mechanics
The simplest form of motion of matter is mechanical motion. DEFINITION: mechanical movement - a change in the relative position of bodies or their parts relative to each other in space
Kinematics of motion of a material point. Movement characteristics.
The position of the material point M in space in this moment time can be specified by the radius vector (see Fig.
Velocity vector. Average and instantaneous speed.
The movements of various bodies differ in that the bodies for the same intervals (equal) of time pass through different
Path with uneven movement.
For a small period of time Dt, the movement is graphically depicted as a rectangle, the height of which is equal to
Acceleration during curvilinear motion (tangential and normal acceleration).
If the trajectory of the movement of a material point is a curved line, then we will call such a movement curvilinear. With such a movement
Angular velocity.
DEFINITION: We will call a rotational motion such a motion in which all points of an absolutely rigid body describe circles whose centers lie on one straight line, called the axis in
angular acceleration.
Vector angular velocity can change both due to a change in the speed of rotation of the body around the axis (in this case
Relationship between linear and angular velocity.
Let the body turn through an angle Dj in a short period of time Dt (Fig. 2.17). A point located at a distance R from the axis passes the path DS = R×Dj. A-priory
Dynamics
A section of mechanics that studies the laws and causes that cause the movement of bodies, i.e. studies the motion of material bodies under the action of forces applied to them. At the heart of classical (Newtonian) fur
Newton's second law.
DEFINITION: The acceleration of any body is directly proportional to the force acting on it and inversely proportional to the mass of the body:
Newton's third law.
Any action of bodies on each other has the character of interaction: if the body M1 acts on the body M2 with some force f12, then the body M2 in turn
Pulse. Law of conservation of momentum.
In a mechanical system consisting of several bodies, there are both forces of interaction between the bodies of the system, which are called internal, and forces of interaction of these bodies with bodies that are not included
work and energy.
Let the body, on which the force acts, pass, moving along a certain trajectory, the path S. In this case, the force either from
Power.
In practice, not only the amount of work done is important, but also the time during which it is done. Of all the mechanisms, the most profitable are those that, in less time, perform
Energy.
We know from experience that bodies are often able to do work on other bodies. DEFINITION: A physical quantity that characterizes the ability of a body or system of bodies to perform
Kinetic energy of the body.
Consider the simplest system, consisting of one particle (material point). Let's write the equation of particle motion
Potential field of forces. The forces are conservative and non-conservative.
If a particle (body) at every point in space is affected by other bodies, then this particle (body) is said to be in the field of forces. Example: 1. Particle near the turn
Potential energy of a body in the field of gravity forces (in the Earth's gravitational field).
The gravitational field of the Earth is a force field, therefore any movement of a body in a force field is accompanied by the performance of work by the forces of this field. To determine the potential energy of a body, finding
Potential energy in the gravitational field (in the field of universal gravitation).
The law of universal gravitation established by Newton reads: DEFINITION: Gravitational force or gravitational force is the force with which two material points attract each other
Potential energy of an elastically deformed body.
Potential energy can be possessed not only by a system of interacting bodies, but also by a separately taken elastically deformed body (for example, a compressed spring, a stretched rod, etc.). In this case
Law of energy conservation.
Without loss of generality, consider a system consisting of two particles with masses m1 and m2. Let the particles interact with each other with forces
Translational motion of a rigid body.
DEFINITION: An absolutely rigid body is a body whose deformations can be neglected under the conditions of the problem under consideration. or Absolutely rigid body
Rotational motion of a rigid body.
DEFINITION: The rotational motion of a rigid body will be called such a motion in which all points of the body move along circles whose centers lie on the same straight line, called
momentum of the body.
To describe the rotational motion, one more quantity is required, called the angular momentum. First
Law of conservation of angular momentum.
FORMULATION: The angular momentum of a closed system of material points remains constant. Note that the angular momentum remains constant for a system subjected to external influences,
The basic equation of the dynamics of rotational motion.
Consider a system of material points, each of which can move, remaining in one of the planes passing through the Z axis (Fig. 4.15). All planes can rotate around the Z axis with angular
Kinetic energy of a rotating rigid body.
1. Consider the rotation of the body around the fixed axis Z. Let us divide the whole body into a set of elementary masses m
The work of external forces during the rotational motion of a rigid body.
Let us find the work done by the forces during the rotation of the body around the fixed axis Z. Let the action on the mass
Lines and tubes of current.
Hydrodynamics studies the motion of liquids, but its laws apply to the motion of gases as well. In a stationary fluid flow, the velocity of its particles at each point in space is a quantity independent of
Bernoulli equation.
We will consider an ideal incompressible fluid in which there is no internal friction (viscosity). Let's single out
Forces of internal friction.
Viscosity is inherent in a real liquid, which manifests itself in the fact that any movement of liquid and gas is spontaneous.
Laminar and turbulent flows.
When enough low speed fluid movement, a layered or laminar flow is observed, when the fluid layers slide relative to each other without mixing. With laminar t
Fluid flow in a round pipe.
When a fluid moves in a round pipe, its velocity is zero at the pipe walls and is maximum at the pipe axis. Assuming
Movement of bodies in liquids and gases.
When symmetrical bodies move in liquids and gases, a force arises drag, directed opposite to the speed of the body. In a laminar flow around the ball, the current line
Kepler's laws.
By the beginning of the 17th century, most scientists were finally convinced of the validity of the heliocentric system of the world. However, the scientists of that time were not clear either the laws of planetary motion or the reasons that determine
Cavendish experience.
The first successful attempt to determine "g" was the measurements carried out by Cavendish (1798), who applied to
The intensity of the gravitational field. The potential of the gravitational field.
Gravitational interaction is carried out through the gravitational field. This field manifests itself in the fact that another body placed in it is under the influence of force. On the "intensity" of gravitational
The principle of relativity.
In sec. 2.1. For mechanical systems The following principle of relativity was formulated: in all inertial frames of reference, all the laws of mechanics are the same. None (fur
Postulates of the special (private) theory of relativity. Lorentz transformations
Einstein formulated two postulates that underlie the special theory of relativity: 1. Physical phenomena in all inertial frames of reference proceed in the same way. None
Consequences from the Lorentz transformations.
The most unexpected consequence of the theory of relativity is the dependence of time on the frame of reference. The duration of events in different systems reference. Let at some point
Interval between events.
In the theory of relativity, the concept of an event is introduced, which is determined by the place where it happened and the time when it happened. An event can be represented by a dot in an imaginary four-dimensional
Equation of harmonic oscillatory motion.
Let a quasi-elastic force act on some body of mass “m”, under the action of which the body acquires acceleration
Graphical representation of harmonic oscillations. Vector diagram.
The addition of several oscillations of the same direction (or, what is the same, the addition of several harmonic functions) is greatly facilitated and becomes clear if the oscillations of the graph are depicted.
Velocity, acceleration and energy of an oscillating body.
Let's return to the formulas for displacement x, speed v and acceleration a of a harmonic oscillatory process. Let we have a body of mass "m", which performs under the action of quasi
Harmonic oscillator.
The system described by the equation, where
damped vibrations.
When deriving the equation of harmonic oscillations, it was assumed that the oscillating point is under the action of only a quasi-elastic force. In any real oscillatory system, there are always forces of resistance
Forced vibrations. Resonance.
In order for the system to perform undamped oscillations, it is necessary to replenish the energy losses of oscillations due to friction from the outside. In order for the energy of the oscillations of the system not to decrease, a force is usually introduced, per
Subject and methods of molecular physics.
Molecular physics is a branch of physics that studies the structure and properties of matter, based on the so-called molecular-kinetic concepts. According to these ideas, any body
Thermodynamic system. System state options. Equilibrium and non-equilibrium state.
DEFINITION: A thermodynamic system is a set of bodies exchanging energy both with each other and with surrounding bodies. An example of a system is a liquid
Ideal gas. Parameters of the ideal gas state.
DEFINITION: An ideal gas is a gas, when considering the properties of which the following conditions are met: a) collisions of molecules of such a gas occur as collisions of elastic balls, dimensions
gas laws.
If we solve the equation of state ideal gas regarding any of the parameters, n
Equation of state of an ideal gas (Mendeleev-Clapeyron equation).
Prior to this, gas processes were considered in which one of the parameters of the state of the gas remained unchanged,
The physical meaning of the universal gas constant.
The universal gas constant has the dimension of work per 1 mole and a temperature of 1°K.
Basic equation of the kinetic theory of gases
If in the previous section the thermodynamic method of research was used, then in this section the statistical method of studying molecular processes will be used. Based on a study with
barometric formula. Boltzmann distribution
It has long been known that the pressure of a gas above the Earth's surface decreases with height. atmospheric pressure for some
Maxwellian velocity distribution of molecules
As a result of collisions, the molecules exchange velocities, and in the case of triple and more complex collisions, the molecule can have temporarily very high and very low velocities. Chaotic movement
transfer phenomena. Mean free path of molecules
In the previous sections, we considered the properties of bodies in thermal equilibrium. This section is devoted to the processes by which the state of equilibrium is established. Such processes
diffusion phenomenon
Diffusion is the process of mutual penetration of molecules of adjoining substances, due to thermal motion. This process is observed in gases, liquids and solids.
The phenomenon of thermal conductivity and viscosity
The phenomenon of thermal conductivity of a substance determines many very important technical processes and is widely used in various calculations. The empirical equation for heat conduction was obtained in French
Thermodynamics
Thermodynamics studies physical phenomena from the point of view of the energy transformations that accompany these phenomena. Thermodynamics originally arose as the science of the mutual transformation of heat into
Internal energy of an ideal gas
An important quantity in thermodynamics is the internal energy of a body. Any body, in addition to mechanical energy, can have a store of internal energy, which is associated with mechanical movement atoms and
work and warmth. First law of thermodynamics
The internal energy of a gas (and other thermodynamic systems) can change mainly due to two processes: doing work on the gas
Work of gas isoprocesses
Let the gas be enclosed in a cylindrical vessel closed with a tightly fitting and easily sliding piston (Fig. 10.3). Etc
Molecular-kinetic theory of heat capacities
The heat capacity of a body C is called a physical quantity numerically equal to the amount of heat that must be imparted to the body to heat it by one degree. If you tell the body to
adiabatic process
Along with isoprocesses, there is an adiabatic process, which is widespread in nature. An adiabatic process is a process that proceeds without heat exchange with the external
Circular reversible processes. Carnot cycle
Mechanical processes have the remarkable reversibility property. For example, a thrown stone, having described a certain trajectory, fell to the ground. If it is thrown back at the same speed, it will describe
The concept of entropy. Entropy of an ideal gas
For the Carnot cycle, from formulas (10.17) and (10.21) it is easy to obtain the relation Q1 /T1 - Q2 /T2 = 0. (10.22)
Second law of thermodynamics
The concept of entropy helped to formulate strictly mathematical patterns that make it possible to determine the direction of thermal processes. A vast body of experimental evidence shows that for
Statistical interpretation of the second law of thermodynamics
The state of a macroscopic body (that is, a body formed by a huge number of molecules) can be specified using volume, pressure, and temperature. This macroscopic state of a gas with a certain
Van der Waals equation
The behavior of real gases at their low densities is well described by the Clapeyron equation:
Critical state of matter
The importance of the van der Waals equation is that it predicts a special state of matter -
Joule-Thomson effect
In a real gas, attractive and repulsive forces act between molecules. Attractive forces are due to the dipole interaction of molecules. Some molecules may be permanent dipots
